
分析 (1)根据:剩余长度=蜡烛总长-燃烧掉的长度,列函数关系式;
(2)根据:面积=长×宽,列函数关系式;
(3)根据:应付款=圆珠笔单件×圆珠笔数量,列函数关系式.
解答 解:(1)l=20-0.1t,常量是20,0.1,变量是t,l;
(2)S=x•$\frac{16-2x}{2}$=-x2+8x,常量是8,变量是x,S;
(3)y=$\frac{18}{12}•x$=1.5x,常量是1.5,变量是x,y.
点评 本题考查了函数关系式:根据实际问题的数量关系用解析式法表示实际问题中两变化的量之间的关系,常量和变量的定义,常量就是在变化过程中不变的量,变量就是可以取到不同数值的量.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{a}^{2}+{b}^{2}+{c}^{2}}$ | B. | $\sqrt{{a}^{2}-{b}^{2}-{c}^{2}}$ | C. | $\sqrt{{a}^{2}-{b}^{2}+{c}^{2}}$ | D. | $\sqrt{-{c}^{2}+{b}^{2}+{a}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
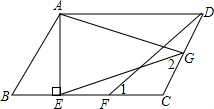 已知,如图,在?ABCD中,AE⊥BC,垂足为E,CE=CD,F为CE的中点,G为CD上的一点,连接DF,EG,AG,∠1=∠2.
已知,如图,在?ABCD中,AE⊥BC,垂足为E,CE=CD,F为CE的中点,G为CD上的一点,连接DF,EG,AG,∠1=∠2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{m=3}\\{n=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{m=3}\\{n=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{m=-3}\\{n=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{m=-3}\\{n=-1}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com