
【题目】方程x(x+3)=x+3的根为( )
A. x=﹣3 B. x=1 C. x1=1,x2=3 D. x1=1,x2=﹣3
科目:初中数学 来源: 题型:
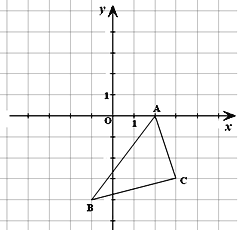
【题目】如图所示的直角坐标系中,解答下列问题:
(1)分别写出A、B两点的坐标;
(2)将△ABC向左平移3个单位长度,再向上平移5个单位长度,画出平移后的△A1B1C1;
(3)求 △A1B1C1的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当![]() 很大时,摸到白球的频率将会接近 .(精确到0.1)
很大时,摸到白球的频率将会接近 .(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)= .
(3)试估算盒子里黑、白两种颜色的球各有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
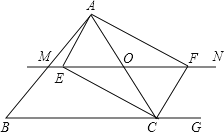
【题目】如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由;
(2)当点O运动到何处时,四边形AECF是矩形?并说出你的理由;
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AECF是正方形.直接写出答案,不需说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
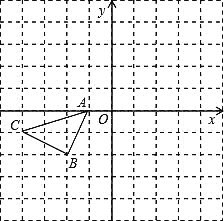
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1.
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
(3)作出点C关于x轴的对称点P.若点P向右平移x(x取整数)个单位长度后落在△A2B2C2的内部,请直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“阳光体育一小时”活动,根据学校实际情况,决定开设A:踢毽子;B:篮球;C:跳绳;D:乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如下两个统计图.请结合图中的信息解答下列问题:
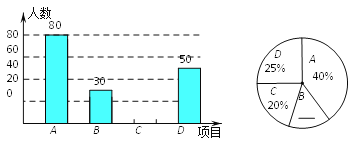
(1)本次共调查了多少名学生?
(2)请将两个统计图补充完整.
(3)若该中学有1200名学生,喜欢篮球运动项目的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BD是矩形ABCD的对角线.
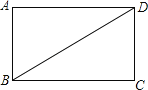
(1)用直尺和圆规作线段BD的垂直平分线,分别交AD、BC于E、F(保留作图痕迹,不写作法和证明).
(2)连结BE,DF,问四边形BEDF是什么四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用等式的性质解方程的步骤:
(1)利用等式的性质________,方程两边同时加(或减)同一个数(或式子)使一元一次方程左边是________,右边是________;
(2)利用等式的性质________,方程两边同时乘未知数的系数的________,使未知数的系数化为1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com