
分析 (1)找出定价为140元时的日销售量,根据总利润=单件利润×销售数量,即可得出商场获得的日盈利;
(2)设商场日盈利达到1500元时,每件商品售价为x元,则每件可盈利(x-120)元,每日销售量为70-(x-130)=200-x(件),根据日盈利=每件利润×销售数量,即可得出关于x的一元二次方程,解之即可得出结论.
解答 解:(1)140-130=10(元),
70-10=60(件),
(140-120)×60=1200(元).
答:每天可销售60件商品,商场获得的日盈利是1200元.
(2)设商场日盈利达到1500元时,每件商品售价为x元,则每件可盈利(x-120)元,每日销售量为70-(x-130)=200-x(件),
根据题意得:(200-x)(x-120)=1500,
整理,得x2-320x+25600=0,
解得:x1=150,x2=170.
答:每件商品售价为150元或170元时,商场日盈利达到1500元.
点评 本题考查了一元二次方程的应用,解题的关键是:(1)根据数量关系,列式计算;(2)根据日盈利=每件利润×销售数量,列出关于x的一元二次方程.


科目:初中数学 来源: 题型:解答题
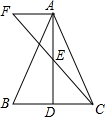 如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F.
如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.14 | B. | $\frac{22}{7}$ | C. | $\sqrt{3}$ | D. | $\sqrt{\frac{4}{9}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的直径,点E是AB上的一点,过点E作CD⊥AB,交⊙O于点C,D,现有下列结论:①若⊙O的半径是2,点E是OB的中点,则CD=2$\sqrt{3}$;②若CD=2$\sqrt{3}$,点E是OB的中点,则⊙O的半径是2;③若∠CAB=30°,则四边形OCBD是菱形;④若四边形OCBD是菱形,则∠CAB=30°,其中正确结论的序号是( )
如图,AB是⊙O的直径,点E是AB上的一点,过点E作CD⊥AB,交⊙O于点C,D,现有下列结论:①若⊙O的半径是2,点E是OB的中点,则CD=2$\sqrt{3}$;②若CD=2$\sqrt{3}$,点E是OB的中点,则⊙O的半径是2;③若∠CAB=30°,则四边形OCBD是菱形;④若四边形OCBD是菱形,则∠CAB=30°,其中正确结论的序号是( )| A. | ①② | B. | ③④ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{25}$ | B. | $\sqrt{4}$ | C. | $\sqrt{5}$ | D. | $\sqrt{0.8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com