
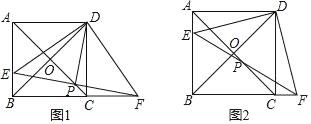
【题目】如图1,在正方形ABCD中,对角线AC,BD交于点O,点E在AB上,点F在BC的延长线上,且AE=CF,连接EF交AC于点P,分别连接DE,DF,DP.
(1)求证:△ADE≌△CDF;
(2)求证:△ADP∽△BDF;
(3)如图2,若PE=BE,则![]() 的值是 (直按写出结果即可).
的值是 (直按写出结果即可).
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)根据SAS证明即可.
(2)想办法证明∠DAP=∠DBF,∠ADP=∠BDF即可解决问题.
(3)如图2中,作PH⊥BC于H.首先证明∠EFB=30°,设HP=HC=m,则PC=![]() m,HF=
m,HF=![]() m,求出CF即可解决问题.
m,求出CF即可解决问题.
(1)∵四边形ABCD是正方形,
∴DA=DC,∠DAE=∠BCD=∠DCF=90°,
∵AE=CF,
∴△ADE≌△CDF(SAS).
(2)作FH∥AB交AC的延长线于H.
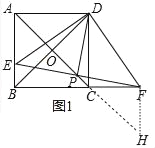
∵四边形ABCD是正方形,
∴∠ACB=∠FCH=45°,
∵AB∥FH,
∴∠HFC=∠ABC=90°,
∴∠FCH=∠H=45°,
∴CF=FH=AE,
∵∠PAE=∠H,∠APE=∠FPH,
∴△APE≌△HPF(AAS),
∴PE=PF,
∵△ADE≌△CDF,
∴DE=DF,∠ADE=∠CDF,∠ADE=∠CDF,
∴∠EFD=∠ADC=90°,
∴△DEF是等腰直角三角形,
∵EP=PF,
∴∠EDP=∠FDP=45°,
∵ADP=∠ADE+∠PDE=∠ADE+45°,∠BDP=∠CDF+∠BDC=∠CDF+45°,
∴∠ADP=∠BDF,
∵∠DAP=∠DBF=45°,
∴△ADP∽△BDF.
(3)如图2中,作PH⊥BC于H.
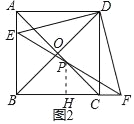
由(2)可知:PE=PF,
∵BE=PE,
∴EF=2BE,
∵∠EBF=90°,
∴sin∠EFB=![]() ,
,
∴∠EFB=30°,
∵PH⊥FH,∠PCH=45°,
∴∠PHC=90°,∠HPC=∠HCP=45°,
∴HP=HC,设HP=HC=m,则![]()
∴CF=![]() m﹣m,
m﹣m,
∴![]()
故答案为: ![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】程大位是我国明朝商人,珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法.书中有如下问题:
一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁.
意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,下列求解结果正确的是( )

A. 大和尚25人,小和尚75人 B. 大和尚75人,小和尚25人
C. 大和尚50人,小和尚50人 D. 大、小和尚各100人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳某学校为构建书香校园,拟购进甲、乙两种规格的书柜放置新购置的图书.已知每个甲种书柜的进价比每个乙种书柜的进价高20%,用3600元购进的甲种书柜的数量比用4200元购进的乙种书柜的数量少4台.
(1)求甲、乙两种书柜的进价;
(2)若该校拟购进这两种规格的书柜共60个,其中乙种书柜的数量不大于甲种书柜数量的2倍.请您帮该校设计一种购买方案,使得花费最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB=AC,CO的延长线交AB于点D.
(1)求证:AO平分∠BAC;
(2)若BC=6,sin∠BAC=![]() ,求AC和CD的长.
,求AC和CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。

(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
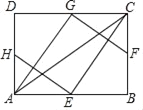
【题目】如图,E、F、G、H分别为矩形ABCD的边AB、BC、CD、DA的中点,连接AC、HE、EC,GA,GF.已知AG⊥GF,AC=![]() ,则AB的长为__________.
,则AB的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△PAB与△PCD均为等腰直角三角形,点C在PB上,若△ABC与△BCD的面积之和为10,则△PAB与△PCD的面积之差为( )
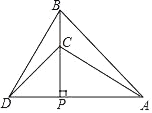
A. 5B. 10C. l5D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,数轴上有A、B两点.
(1)线段AB的中点表示的数是 ;
(2)线段AB的长度是 ;
(3)若A、B两点问时向右运动,A点速度是每秒3个单位长度,B点速度是每秒2个单位长度,问经过几秒时AB=2?
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com