
ĄžĚâÄżĄżÔÄśÁ˛ÄÁĎŁşČçÍź1ŁŹČôľăPĘÇĄŃOÍâľÄŇťľăŁŹĎßśÎPO˝ťĄŃOÓÚľăAŁŹÔňPAł¤ĘÇľăPÓëĄŃOÉϸ÷ľăÖŽźäľÄ×îśĚžŕŔ룎
Ö¤Ă÷ŁşŃÓł¤PO˝ťĄŃOÓÚľăBŁŹĎÔČťPBŁžPAŁŽ
ČçÍź2ŁŹÔÚĄŃOÉĎČÎČĄŇťľăCŁ¨ÓëľăAŁŹB˛ťÖغϣŠŁŹÁŹ˝áPCŁŹOCŁŽ
ĄßPOŁźPC+OCŁŹ
ÇŇPO=PA+OAŁŹOA=OCŁŹ
ĄŕPAŁźPC
ĄŕPA ł¤ĘÇľăPÓëĄŃOÉϸ÷ľăÖŽźäľÄ×îśĚžŕŔ룎
ÓÉ´ËżÉŇԾþ˝ŐćĂüĚ⣺ԲÍâŇťľăÓëÔ˛Éϸ÷ľăÖŽźäľÄ×îśĚžŕŔëĘÇŐâľăľ˝Ô˛ĐľĞŕŔëÓë°ëžśľÄ˛îŁŽÇëÓĂÉĎĘöŐćĂüĚâ˝âžöĎÂÁĐÎĘĚ⣎
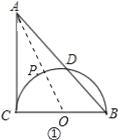
Ł¨1ŁŠČçÍź3ŁŹÔÚRtĄ÷ABCÖĐŁŹĄĎACB=90ĄăŁŹAC=BC=2ŁŹŇÔBCÎŞÖąžśľÄ°ëÔ˛˝ťABÓÚDŁŹPĘÇ![]() ÉĎľÄŇť¸öśŻľăŁŹÁŹ˝ÓAPŁŹÔňAPł¤ľÄ×îĐĄÖľĘÇĄĄ ĄĄŁŽ
ÉĎľÄŇť¸öśŻľăŁŹÁŹ˝ÓAPŁŹÔňAPł¤ľÄ×îĐĄÖľĘÇĄĄ ĄĄŁŽ
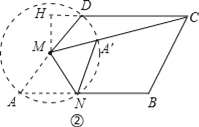
Ł¨2ŁŠČçÍź4ŁŹÔÚąßł¤ÎŞ2ľÄÁâĐÎABCDÖĐŁŹĄĎA=60ĄăŁŹMĘÇADąßľÄÖо㣏ľăNĘÇABąßÉĎŇťśŻľăŁŹ˝ŤĄ÷AMNŃŘMNËůÔÚľÄÖąĎߡŐ۾þ˝Ą÷AĄäMNŁŹÁŹ˝ÓAĄäCŁŹ˘ŮÇóĎßśÎAĄŻMľÄł¤śČŁť ˘ÚÇóĎßśÎAĄäCł¤ľÄ×îĐĄÖľŁŽ

Ąž´đ°¸ĄżŁ¨1ŁŠ![]() Ł¨2ŁŠ˘Ů1˘Ú
Ł¨2ŁŠ˘Ů1˘Ú![]()
Ąž˝âÎöĄżĘÔĚâˇÖÎö:Ł¨1ŁŠÓÉÔ˛ÍâŇťľăÓëÔ˛Éϸ÷ľăÖŽźäľÄ×îśĚžŕŔëĘÇŐâľăľ˝Ô˛ĐľĞŕŔëÓë°ëžśľÄ˛îżÉľĂ˝áÂŰŁť
Ł¨2ŁŠ˘ŮŔűÓáŐŰľÄĐÔÖĘşÍÁâĐÎľÄĐÔÖʿɾóö˝áÂŰŁť
˘ÚŔűÓâپĽáÂŰŇ׾þăAĄäÔÚŇÔľăMÎŞÔ˛ĐÄŁŹ1ÎŞ°ëžśľÄÔ˛ÉĎŁŹÔŮŔűÓĂÁâĐÎľÄĐÔÖĘşÍČń˝ÇČý˝ÇşŻĘýľĂDHŁŹMHŁŹŇ׾ĂCHŁŹÓÉš´šÉś¨ŔíľĂCMŁŹÇóľĂAĄäCŁŽ
˝â:Ł¨1ŁŠÁŹ˝ÓAOÓëĄŃOĎཝÓÚľăPŁŹČçÍź˘ŮŁŹÓÉŇŃÖŞś¨ŔíżÉÖŞŁŹ
´ËĘąAP×îśĚŁŹ
ĄßĄĎACB=90ĄăŁŹAC=BC=2ŁŹBCÎŞÖąžśŁŹ
ĄŕPO=CO=1ŁŹ
ĄŕAO=![]() =
=![]() =
=![]() ŁŹ
ŁŹ
ĄŕAP=![]() Š1ŁŹ
Š1ŁŹ
šĘ´đ°¸ÎŞŁş![]() Š1Łť
Š1Łť
Ł¨2ŁŠ˘ŮĄß˝ŤĄ÷AMNŃŘMNËůÔÚľÄÖąĎߡŐ۾þ˝Ą÷AĄäMNŁŹÓɡŐŰľÄĐÔÖʿɾãş
AĄäM=AMŁŹ
ĄßMĘÇADąßľÄÖо㣏ËÄąßĐÎABCDÎŞÁâĐÎŁŹąßł¤ÎŞ2ŁŹ
ĄŕAM=1ŁŹ
ĄŕAĄäM=1Łť
˘ÚÓɢŮÖŞŁŹľăAĄäÔÚŇÔľăMÎŞÔ˛ĐÄŁŹ1ÎŞ°ëžśľÄÔ˛ÉĎŁŹ
ÁŹ˝ÓCM˝ťÔ˛MÓÚľăAĄäŁŹšýľăMĎňCDľÄŃÓł¤Ďß×÷´šĎߣŹ´š×ăÎŞľăHŁŹČçÍź˘ÚŁŹ
ĄßĄĎA=60ĄăŁŹËÄąßĐÎABCDÎŞÁâĐÎŁŹ
ĄŕĄĎHDM=60ĄăŁŹ
ÔÚRtĄ÷MHDÖĐŁŹ
DH=DMcosĄĎHDM=![]() ŁŹ
ŁŹ
MH=DMsinĄĎHDM=![]() ŁŹ
ŁŹ
ĄŕCH=CD+DH=2+![]() =
=![]() ŁŹ
ŁŹ
ÔÚRtĄ÷CHMÖĐŁŹ
CM=![]() =
=![]() =
=![]() ŁŹ
ŁŹ
ĄŕAĄäC=![]() Š1ŁŽ
Š1ŁŽ


 ĂűĘŚÖ¸ľźĆÚÄŠłĺ´ĚžíĎľÁĐ´đ°¸
ĂűĘŚÖ¸ľźĆÚÄŠłĺ´ĚžíĎľÁĐ´đ°¸
| Äęźś | ¸ßÖĐżÎłĚ | Äęźś | łőÖĐżÎłĚ |
| ¸ßŇť | ¸ßŇťĂâˇŃżÎłĚÍĆźöŁĄ | łőŇť | łőŇťĂâˇŃżÎłĚÍĆźöŁĄ |
| ¸ßśţ | ¸ßśţĂâˇŃżÎłĚÍĆźöŁĄ | łőśţ | łőśţĂâˇŃżÎłĚÍĆźöŁĄ |
| ¸ßČý | ¸ßČýĂâˇŃżÎłĚÍĆźöŁĄ | łőČý | łőČýĂâˇŃżÎłĚÍĆźöŁĄ |
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżĄ÷CDEşÍĄ÷AOBĘÇÁ˝¸öľČŃüÖą˝ÇČý˝ÇĐÎŁŹĄĎCDEŁ˝ĄĎAOBŁ˝90ĄăŁŹDCŁ˝DEŁ˝1ŁŹOAŁ˝OBŁ˝aŁ¨aŁž1ŁŠŁŽ
Ł¨1ŁŠ˝ŤĄ÷CDEľÄśĽľăDÓëľăOÖغϣŹÁŹ˝ÓAEŁŹBCŁŹČĄĎßśÎBCľÄÖĐľăMŁŹÁŹ˝ÓOMŁŽ
˘ŮČçÍź1ŁŹČôCDŁŹDEˇÖąđÓëOAŁŹOBąßÖغϣŹÔňĎßśÎOMÓëAEÓĐÔőŃůľÄĘýÁżšŘĎľŁżÇëÖą˝ÓĐ´łöÄăľÄ˝ášűŁť
˘ÚČçÍź2ŁŹČôCDÔÚĄ÷AOBÄÚ˛żŁŹÇëÄăÔÚÍź2ÖĐťłöÍęŐűÍźĐÎŁŹĹĐśĎOMÓëAEÖŽźäľÄĘýÁżšŘĎľĘǡńÓй䝯ŁżĐ´łöÄăľÄ˛ÂĎ룏˛˘źÓŇÔÖ¤Ă÷Łť
˘Ű˝ŤĄ÷CDEČĆľăOČÎŇâתśŻŁŹĐ´łöOMľÄČĄÖľˇśÎ§Ł¨ÓĂşŹaĘ˝×ÓąíĘžŁŠŁť
Ł¨2ŁŠĘǡń´ćÔÚąßł¤×î´óľÄĄ÷AOBŁŹĘšĄ÷CDEľÄČý¸öśĽľăˇÖąđÔÚĄ÷AOBľÄČýĚőąßÉĎŁ¨śź˛ťÓ뜼ľăÖغϣŠŁżČçšű´ćÔÚŁŹÇëÄăťłö´ËĘąľÄÍźĐÎŁŹ˛˘Çółöąßł¤aľÄÖľŁťČçšű˛ť´ćÔÚŁŹÇëËľĂ÷ŔíÓÉŁŽ

˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżÔÚ![]() ÖĐŁŹ
ÖĐŁŹ ![]() ÎŞ
ÎŞ![]() ąßÉĎŇťľăŁŹšýľă
ąßÉĎŇťľăŁŹšýľă![]() ×÷
×÷![]() ˝ť
˝ť![]() ÓÚľă
ÓÚľă![]() ŁŹŇÔ
ŁŹŇÔ![]() ÎŞŐŰĎߣŹ˝Ť
ÎŞŐŰĎߣŹ˝Ť![]() ˇŐŰŁŹÉčËůľĂľÄ
ˇŐŰŁŹÉčËůľĂľÄ![]() ÓëĚÝĐÎ
ÓëĚÝĐÎ![]() ÖŘľţ˛żˇÖľÄĂćťýÎŞ
ÖŘľţ˛żˇÖľÄĂćťýÎŞ![]() ŁŽ
ŁŽ
Ł¨![]() ŁŠČçÍźŁ¨ź×ŁŠŁŹČô
ŁŠČçÍźŁ¨ź×ŁŠŁŹČô![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹÔň
ŁŹÔň![]() ľÄ־Ϊ__________ŁŽ
ľÄ־Ϊ__________ŁŽ
Ł¨![]() ŁŠČçÍźŁ¨ŇŇŁŠŁŹČô
ŁŠČçÍźŁ¨ŇŇŁŠŁŹČô![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ÎŞ
ÎŞ![]() Öо㣏Ôň
Öо㣏Ôň![]() ľÄ־Ϊ__________ŁŽ
ľÄ־Ϊ__________ŁŽ
Ł¨![]() ŁŠČô
ŁŠČô![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹÉč
ŁŹÉč![]() ŁŽ
ŁŽ
˘ŮÇó![]() Óë
Óë![]() ľÄşŻĘý˝âÎöĘ˝ŁŽ
ľÄşŻĘý˝âÎöĘ˝ŁŽ
˘Ú![]() ĘǡńÓĐ×î´óÖľŁŹČôÓĐŁŹÇółö
ĘǡńÓĐ×î´óÖľŁŹČôÓĐŁŹÇółö![]() ľÄ×î´óÖľŁťČôĂťÓĐŁŹÇëËľĂ÷ŔíÓÉŁŽ
ľÄ×î´óÖľŁťČôĂťÓĐŁŹÇëËľĂ÷ŔíÓÉŁŽ
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżÔÚŐýˇ˝ĐÎÍř¸ńÖĐŁŹĂż¸öĐĄŐýˇ˝ĐξĹ߳¤śźÎŞ1¸öľĽÎťł¤śČŁŹĄ÷ABCľÄČý¸öśĽľăľÄÎťÖĂČçÍźËůĘžŁŹĎÖ˝ŤĄ÷ABCĆ˝ŇĆşóľĂĄ÷DEFŁŹĘšľăAľÄśÔÓŚľăÎŞľăDŁŹľăBľÄśÔÓŚľăÎŞľăEŁŽ
Ł¨1ŁŠťłöĄ÷DEFŁť
Ł¨2ŁŠÁŹ˝ÓADĄ˘BEŁŹÔňĎßśÎADÓëBEľÄšŘĎľĘÇ Łť
Ł¨3ŁŠÇóĄ÷DEFľÄĂćťýŁŽ

˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżÄłľŘĹŠĂńŇťÖąąŁłÖ×ĹśŹÖÖÓͲ˾ÄĎ°šßŁŹŔűÓĂĹŠĎĐśŹÖÖŇťźžÓͲˣŽ¸ĂľŘĹŠŇľ˛żĂĹśÔ2017ÄęľÄÓͲË×ŃÉú˛úłÉąžĄ˘ĘĐłĄźŰ¸ńĄ˘ÖÖÖ˛ĂćťýşÍ˛úÁżľČ˝řĐĐÁËľ÷˛éÍłźĆŁŹ˛˘ťćÖĆÁËČçĎÂľÄÍłźĆąíÓëÍłźĆÍź(ČçÍź)Łş
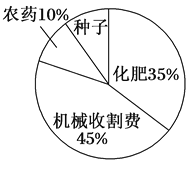
ÿĜÉú˛úłÉąž | ÿĜ˛úÁż | ÓͲË×ŃĘĐłĄźŰ¸ń | ÖÖÖ˛Ăćťý |
110ÔŞ | 130ǧżË | 3ÔŞ/ǧżË | 500 000Äś |
Çë¸ůžÝŇÔÉĎĐĹϢ˝â´đĎÂÁĐÎĘĚ⣺
(1)ÖÖÖ˛ÓͲËÿĜľÄÖÖ×ӳɹžĘÇśŕÉŮÔŞŁż
(2)ĹŠĂńśŹÖÖÓͲËÿĜťńŔűśŕÉŮÔŞŁż
(3)2017Äę¸ĂľŘČŤĎŘĹŠĂńśŹÖÖÓͲ˾Ä×ÜťńŔűĘÇśŕÉŮÔŞŁż(˝ášűÓĂżĆѧźÇĘýˇ¨ąíĘž)
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżÄł˛ÍĚüÖĐŁŹŇťŐĹ×Ŕ×ÓżÉ×ř6ČËŁŹÓĐČçÍźËůĘžľÄÁ˝Öְڡš˝Ę˝Łş

Ł¨1ŁŠľąÓĐnŐĹ×Ŕ×ÓĘąŁŹÁ˝Öְڡš˝Ę˝¸÷ÄÜ×řśŕÉŮČËŁż
Ł¨2ŁŠŇťĚěÖĐÎç˛ÍĚüŇŞ˝Ó´ý98ÎťšËżÍš˛ÍŹžÍ˛ÍŁŹľŤ˛ÍĚüÖťÓĐ25ŐĹŐâŃůľÄ˛Í×Ŕ.ČôÄăĘÇŐâ¸ö˛ÍĚüľÄžŔíŁŹÄă´ňËăŃĄÔńÄÄÖÖˇ˝Ę˝Ŕ´°ÚˇĹ˛Í×ŔŁżÎŞĘ˛Ă´Łż
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżŇť°ăÇéżöĎÂ![]() ˛ťłÉÁ˘,ľŤÓĐĐŠĘýżÉŇÔĘšľĂËüłÉÁ˘,ŔýČ磺a=b=0.ÎŇĂÇłĆĘšľĂ
˛ťłÉÁ˘,ľŤÓĐĐŠĘýżÉŇÔĘšľĂËüłÉÁ˘,ŔýČ磺a=b=0.ÎŇĂÇłĆĘšľĂ![]() łÉÁ˘ľÄŇťśÔĘýa,bÎŞĄ°şÍĐłĘýśÔĄą,źÇÎŞŁ¨a,bŁŠ.
łÉÁ˘ľÄŇťśÔĘýa,bÎŞĄ°şÍĐłĘýśÔĄą,źÇÎŞŁ¨a,bŁŠ.
(1)Čô(3,x)ĘÇĄ°şÍĐłĘýśÔĄąŁŹÇóxľÄÖľŁť
(2)Čô(m,n)ĘÇĄ°şÍĐłĘýśÔĄą,Çó´úĘýĘ˝![]() ľÄÖľŁť
ľÄÖľŁť
(3)ÓĐŇť¸öĄ°şÍĐłĘýśÔĄą(a,b)ŁŹÂú×ăaŁb=1ŁŹÇóaŁŹbľÄÖľ.
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżśţ´ÎşŻĘýy=ax2+bx+cŁ¨aĄŮ0ŁŠľÄ˛żˇÖÍźĎóČçÍźËůĘžŁŹĆ䜼ľă×řąęÎŞŁ¨1ŁŹnŁŠŁŹÇŇÓëxÖáľÄŇť¸ö˝ťľăÔÚŁ¨3ŁŹ0ŁŠşÍŁ¨4ŁŹ0ŁŠÖŽźäŁŹÔňĎÂÁĐ˝áÂŰŁş
˘Ůac![]()
˘ÚaŠb+cŁž0Łť
˘Űľą![]() ĘąŁŹyËćxľÄÔö´óśřÔö´ó
ĘąŁŹyËćxľÄÔö´óśřÔö´ó
ČôŁ¨Š![]() ŁŹy1ŁŠŁŹŁ¨
ŁŹy1ŁŠŁŹŁ¨![]() ŁŹy2ŁŠĘÇĹ×ÎďĎßÉĎľÄÁ˝ľăŁŹÔňy1
ŁŹy2ŁŠĘÇĹ×ÎďĎßÉĎľÄÁ˝ľăŁŹÔňy1![]() y2Łť
y2Łť
˘ÜŇťÔŞśţ´Îˇ˝łĚax2+bx+c=nŠ1ÓĐÁ˝¸ö˛ťĎŕľČľÄĘľĘý¸ůŁŽ
ĆäÖĐŐýȡ˝áÂ۾ĸöĘýĘÇŁ¨ĄĄĄĄŁŠ

A. 1 B. 2 C. 3 D. 4
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżÄÜĹĐś¨ËÄąßĐÎ![]() ĘÇĆ˝ĐĐËÄąßĐÎľÄĘÇŁ¨ ŁŠ
ĘÇĆ˝ĐĐËÄąßĐÎľÄĘÇŁ¨ ŁŠ
A.ABĄÎCDŁŹ![]() B. ABĄÎCDŁŹ
B. ABĄÎCDŁŹ![]()
C.![]() ŁŹ
ŁŹ![]() D.
D.![]() ŁŹ
ŁŹ![]()
˛éż´´đ°¸şÍ˝âÎö>>
°ŮśČÖÂĐĹ - ÁˇĎ°˛áÁĐąí - ĘÔĚâÁĐąí
şţąąĘĄťĽÁŞÍřÎĽˇ¨şÍ˛ťÁźĐĹϢžŮą¨Ć˝Ě¨ | ÍřÉĎÓĐşŚĐĹϢžŮą¨×¨Çř | ľçĐĹՊƞٹ¨×¨Çř | ÉćŔúʡĐéÎŢÖ÷ŇĺÓĐşŚĐĹϢžŮą¨×¨Çř | ÉćĆóÇÖȨžŮą¨×¨Çř
ÎĽˇ¨şÍ˛ťÁźĐĹϢžŮą¨ľçť°Łş027-86699610 žŮą¨ÓĘĎ䣺58377363@163.com