
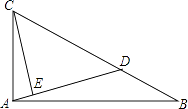
【题目】如图,已知点D是Rt△ABC的斜边BC上的一点,tanB= ![]() ,BC=3BD,CE⊥AD,则
,BC=3BD,CE⊥AD,则 ![]() = .
= . 
【答案】![]()
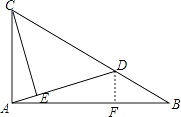
【解析】解:过点D作DF⊥AB于点F, ∵∠CAB=90°,DF⊥AB,
∴AC∥DF,
∴ ![]() =
=
∵BC=3BD,
∴ ![]() =
= ![]() ,
,
∴AF=kBF
∵tanB= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴DF= ![]() FB,
FB,
∴ ![]() ,
,
∵CE⊥AD,
∴tan∠ACE= ![]() ,
,
∵∠CAE+∠ACE=90°,∠CAE+∠DAB=90°,
∴∠ACE=∠DAF,
∴tan∠ACE=tan∠DAF= ![]() .
.
所以答案是: ![]() .
.
【考点精析】本题主要考查了勾股定理的概念和相似三角形的判定与性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】观察下列等式:
第一个等式:a1=![]() =
=![]() -
-![]()
第二个等式:a2= =
=![]() -
-![]()
第三个等式:a3= =
=![]() -
-![]()
第四个等式:a4= =
=![]() -
-![]()
按上述规律,回答下列问题:
(1)请写出第六个等式:a6=_____=_____;
(2)用含n的代数式表示第n个等式:an=_____=_____;
(3)a1+a2+a3+a4+a5+a6=_____(得出最简结果);
(4)计算:a1+a2+…+an.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育老师对自己任教的55名男生进行一百米摸底测试,若规定男生成绩为16秒合格,下表是随机抽取的10名男生分A、B两组测试的成绩与合格标准的差值(比合格标准多的秒数为正,少的秒数为负).
A 组 | ﹣1.5 | +1.5 | ﹣1 | ﹣2 | ﹣2 |
B组 | +1 | +3 | ﹣3 | +2 | ﹣3 |
(1)请你估算从55名男生中合格的人数大约是多少?
(2)通过相关的计算,说明哪个组的成绩比较均匀;
(3)至少举出三条理由说明A组成绩好于B组成绩,或找出一条理由来说明B组好于A组.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D、E分别在边AC、BC上(不与点A、B、C重合),点P是直线AB上的任意一点(不与点A、B重合).设∠PDA=x,∠PEB=y,∠DPE=m,∠C=n.
(1)如图,当点P在线段AB上运动,且n=90°时
①若PD∥BC,PE∥AC,则m=_____;
②若m=50°,求x+y的值.
(2)当点P在直线AB上运动时,直接写出x、y、m、n之间的数量关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
在△ABC中,AB=AC,点P为BC所在直线上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.当P在BC边上时(如图1),求证:PD+PE=CF.

图① 图② 图③
证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.(不要证明)
【变式探究】
当点P在CB延长线上时,其余条件不变(如图3).试探索PD、PE、CF之间的数量关系并说明理由.
请运用上述解答中所积累的经验和方法完成下列两题:
【结论运用】
如图4,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;
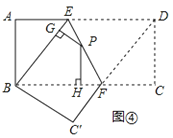
【迁移拓展】
在直角坐标系中.直线l1:y=![]() 与直线l2:y=2x+4相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为1.求点P的坐标.
与直线l2:y=2x+4相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为1.求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作探究:已知在纸面上有一数轴(如图所示).
![]()
左右折叠纸面,折痕所在的直线与数轴的交点为“对折中心点”
操作一:
(1)左右折叠纸面,使1表示的点与-1表示的点重合,则-3表示的点与 表示的点重合;
操作二:
(2)左右折叠纸面,使-1表示的点与3表示的点重合,回答以下问题:
①对折中心点所表示的数为 ,对折后5表示的点与数 表示的点重合;
②若数轴上A.B两点之间距离为11(A在B的左侧),且A.B两点经折叠后重合,求A.B两点表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com