Question

18．如图，矩形ABCD中，AB=a，BC=b，动点P从A点出发，按A→B→C的方向在AB和BC上移动，记PA=x，点D到直线PA的距离为y，且y关于x的函数图象大致如图：
（1）a=3，b=4；
（2）求y关于x的函数关系式，并直接写出x的取值范围；
（3）当△PCD的面积是△ABP的面积的$\frac{1}{3}$时，求y的值．

Answer 1

分析 （1）根据函数的图象，即可得出a、b的值；
（2）分点P在线段AB上跟点P在线段BC上讨论，依据相似三角形的性质，即可得出y与x之间的关系；
（3）由等高三角形的面积比等于底边长之比，可得出BP的长，根据勾股定理得出x的值，代入到（2）中的关系式中即可求出y的值．

解答 解：（1）当点P在线段AB上时，D到AB的距离为AD，
由函数图象可看出，AD=4，即BC=b=4，
当点P运动到线段BC上时，D到AB的距离出现变化，
由函数图象可看出，AB=3=a．
故答案为：3；4．
（2）①当点P在线段AB上时，有0≤AP≤AB，即0≤x≤3，
此时y=4．
②当点P在线段BC上时，连接AC，过点D作DE⊥AP于点E，如图，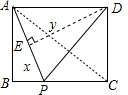

由勾股定理可得：AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5．
∵此时P点过B点向C点运动，
∴AB＜AP≤AC，即3＜x≤5．
∵AD∥BC，
∴∠DAE=∠APB，
又∵∠ABP=∠DEA=90°，
∴△DAE∽△APB，
∴$\frac{BE}{AB}$=$\frac{AD}{AP}$，即$\frac{y}{3}$=$\frac{4}{x}$，
∴y=$\frac{12}{x}$．
综合①②得：y=$\left\{\begin{array}{l}{4（0≤x≤3）}\\{\frac{12}{x}（3＜x≤5）}\end{array}\right.$．
（3）∵△PCD的面积是△ABP的面积的$\frac{1}{3}$，且两三角形等高，
∴BP=3PC，
∵BP+PC=BC=4，
∴BP=3，
由勾股定理可得：x=$\sqrt{A{P}^{2}+B{P}^{2}}$=3$\sqrt{2}$，
将x=3$\sqrt{2}$代入，得y=$\frac{12}{3\sqrt{2}}$=2$\sqrt{2}$．
故当△PCD的面积是△ABP的面积的$\frac{1}{3}$时，y的值为2$\sqrt{2}$．

点评 本题考查了动点问题的函数图象、相似三角形的判定及性质和勾股定理，解题的关键是：（1）能看懂函数图象并结合题意找出a、b的值；（2）分P点在线段AB和BC上讨论，借助到了相似三角形的判定及性质；（3）根据等高三角形的面积比等于底边长之比，得出BP的长，根据勾股定理得出x的值．