
【题目】完成下列各题:
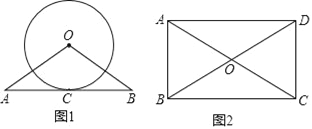
(1)如图,已知直线AB与⊙O相切于点C,且AC=BC,求证:OA=OB.
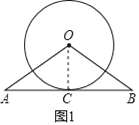
(2)如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB=3,求AC的长.
【答案】(1)证明见解析;(2)6cm
【解析】试题分析:(1)根据线段垂直平分线的性质:线段垂直平分线上的点到两端点的距离相等来证明;
(2)根据矩形性质得出AC=BD,OA=OB,求出∠AOB=60°,得出△AOB是等边三角形,求出∠ADB=30°,得出AC=BD=2AB=6cm即可.
(1)证明:连接OC,
∵直线AB与⊙O相切于点C,
∴OC⊥AB,
又∵AC=BC,
∴OC垂直平分AB,
∴OA=OB;
(2)证明:∵四边形ABCD是矩形,
∴AC=BD,OA=OC=![]() AC,BO=DO=
AC,BO=DO=![]() BD,∠BAD=90°,
BD,∠BAD=90°,
∴OA=OB,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴∠ABO=60°,∠ADB=30°,
∴AC=BD=2AB=6cm.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】2017年度中央机关及其直属机构公务员招考网上报名已经结束,据初步统计,网上报名人数约有211.5万人,数据211.5万用科学记数法可表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
【问题情境】金老师给“数学小达人”小明和小军提出这样一个问题:
如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC.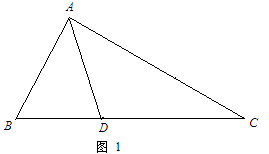
【证明思路】小明的证明思路是:如图2,在AC上截取AE=AB,连接DE.……
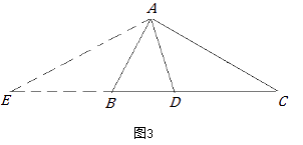
小军的证明思路是:如图3,延长CB至点E,使BE=AB,连接AE.可以证得:AE=DE.……
(1)请你从他们的思路中,任意选择一种思路继续完成下一步的证明.
(2)【变式探究】如图4,金老师把“AD是∠BAC的平分线”改成“AD是BC边上的高”,其它条件不变,那么AB+BD=AC还成立吗?若成立,请证明;若不成立,写出正确结论,并说明理由.
(3)【迁移拓展】如图5,△ABC中,∠B=2∠C.求证:AC2—AB2=AB×BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商店某天销售了14件衬衫,其领口尺寸统计如表:
领口尺寸(单位:cm) | 38 | 39 | 40 | 41 | 42 |
件数 | 1 | 5 | 3 | 3 | 2 |
则这14件衬衫领口尺寸的众数与中位数分别是( )
A.39cm、39cm
B.39cm、39.5cm
C.39cm、40cm
D.40cm、40cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
频数分布表
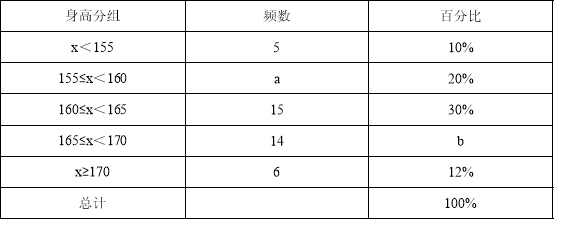
(1)填空:a= ,b= ;
(2)补全频数分布直方图;
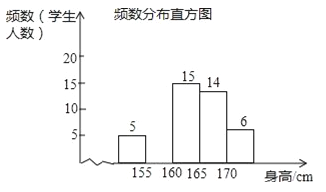
(3)该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 图像的一部分,其对称轴为x=-l,且过点(-3,0).下列说法:①abc<0;②2a-b=O;③4a+2b+c<0;④若(-5,y1),
图像的一部分,其对称轴为x=-l,且过点(-3,0).下列说法:①abc<0;②2a-b=O;③4a+2b+c<0;④若(-5,y1),![]() 是抛物线上两点,则y1>y2,其中说法正确的有( )
是抛物线上两点,则y1>y2,其中说法正确的有( )
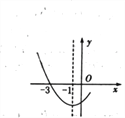
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
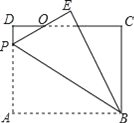
【题目】如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com