
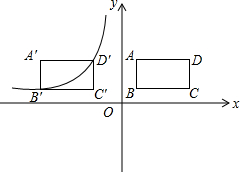
 如图所示,在平面直角坐标系中,矩形ABCD,AB=2,BC=4,点B(1,1).
如图所示,在平面直角坐标系中,矩形ABCD,AB=2,BC=4,点B(1,1).分析 (1)根据B点的坐标和矩形的性质得出即可;
(2)根据题意得出B′和D′的坐标,代入函数解析式求出a的值,即可得出函数的解析式.
解答 解:(1)∵矩形ABCD,AB=2,BC=4,点B(1,1).
∴A(1,3),C(5,1),D(5,3),
故答案为:(1,3),(5,1),(5,3);
(2)根据题意得:B′(1-a,1),D′(5-a,3),
∵点B′,D′恰好同时落在反比例函数y=$\frac{k}{x}$(x<0)的图象上,
∴(1-a)×1=(5-a)×3,
解得:a=7,
∴B′(-6,1),
∴y=-$\frac{6}{x}$.
点评 本题考查了矩形的性质,用待定系数法求反比例函数的解析式,坐标与图形性质和平移等知识点,能求出B′的坐标是解此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | m≤2 | B. | m<2 | C. | m≤2且m≠1 | D. | m<2且m≠1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
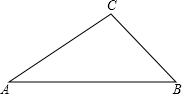 已知:如图,在△ABC中,∠ABC=45°,tanA=$\frac{3}{4}$,AB=14,
已知:如图,在△ABC中,∠ABC=45°,tanA=$\frac{3}{4}$,AB=14,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
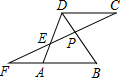 如图,点P是菱形ABCD对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F,则线段PC、PE、PF之间存在的数量关系是( )
如图,点P是菱形ABCD对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F,则线段PC、PE、PF之间存在的数量关系是( )| A. | 2PC=PE+PF | B. | 2PC=PE•PF | C. | PC2=PE•PF | D. | PC2=$\frac{PF}{PE}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
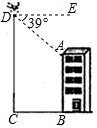 如图,某校无人机兴趣小组借助无人机测量教学楼的高度AB,无人机在离教学楼底部B处16米的C处垂直上升31米至D处,测得教学楼顶A处的俯角为39°,求教学楼的高度AB.(结果精确到0.1米)【参考数据:sin39°=0.63,cos39°=0.78,tan39°=0.81】
如图,某校无人机兴趣小组借助无人机测量教学楼的高度AB,无人机在离教学楼底部B处16米的C处垂直上升31米至D处,测得教学楼顶A处的俯角为39°,求教学楼的高度AB.(结果精确到0.1米)【参考数据:sin39°=0.63,cos39°=0.78,tan39°=0.81】查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com