
【题目】已知抛物线![]()
(1)填空:抛物线的顶点坐标是( , ),对称轴是 ;
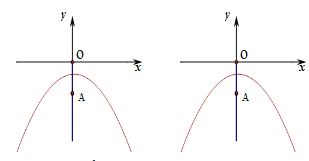
(2)已知y轴上一点A(0,-2),点P在抛物线上,过点P作PB⊥x轴,垂足为B.若△PAB是等边三角形,求点P的坐标;
(3)在(2)的条件下,点M在直线AP上.在平面内是否存在点 N,使以点O、点A、点M、点N为顶点的四边形为菱形?若存在,直接写出所有满足条件的点N的坐标;若不存在,请说明理由.
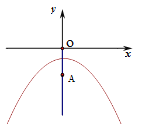
【答案】(1)、顶点(0,-1),对称轴:y轴;(2)、P1(![]() ) P2(
) P2(![]() );(3)、当点P的坐标为(
);(3)、当点P的坐标为(![]() ) 时:N1(
) 时:N1(![]() ) N2(-
) N2(-![]() ),N3(
),N3(![]() );当点P的坐标为(
);当点P的坐标为(![]() )时,N4(
)时,N4(![]() ), N5(
), N5(![]() ) , N6(
) , N6(![]() )
)
【解析】
试题分析:(1)、根据解析式可求得顶点坐标和对称轴;(2)、根据等边三角形的性质来进行求解,本题可以首先设出点P的坐标,然后求出PA、PB、AB的长度,然后根据等边三角形的性质进行计算;(3)、分两种情况根据菱形的性质求出点N的坐标.
试题解析:(1)、顶点(0,-1), 对称轴: y轴(或直线 x = 0)
(2)、P1(![]() ) P2(
) P2(![]() )
)
(3)、当点P的坐标为(![]() ) 时:N1(
) 时:N1(![]() ) N2(-
) N2(-![]() ),N3(
),N3(![]() );当点P的坐标为(
);当点P的坐标为(![]() )时,N4(
)时,N4(![]() ), N5(
), N5(![]() ) , N6(
) , N6(![]() ).
).


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
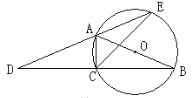
【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连结AC,CE。
(1)求证:∠B=∠D;
(2)若AB= ![]() ,BC-AC=2,求CE的长。
,BC-AC=2,求CE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以△ABC的边AB,AC向外作等边△ABD和等边△ACE,线段BE与CD相交于点O,连接OA.
(1)请你完成图形(尺规作图,不写作法,保留作图痕迹);

(2)求证:BE=DC;
(3)求证:OA平分∠DOE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年春节期间(1月27日至2月2日),长春龙嘉国际机场保障航班起降1695架次,运送旅客大约228600人次,228600这个数用科学记数法表示为( )
A.22.86×104
B.2.286×105
C.2.286×106
D.0.2286×106
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com