
分析 根据题目中的式子可以得到关于A和B的二元一次方程组,从而可以求得A、B的值.
解答 解:∵$\frac{A}{x+3}+\frac{B}{x-2}$计算结果是$\frac{3x+4}{(x+3)(x-2)}$,
∴$\frac{A}{x+3}+\frac{B}{x-2}=\frac{3x+4}{(x+3)(x-2)}$,
∴$\frac{A(x-2)+B(x+3)}{(x+3)(x-2)}=\frac{3x+4}{(x+3)(x-2)}$,
∴$\frac{(A+B)x+(-2A+3B)}{(x+3)(x-2)}=\frac{3x+4}{(x+3)(x-2)}$,
∴$\left\{\begin{array}{l}{A+B=3}\\{-2A+3B=4}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{A=1}\\{B=2}\end{array}\right.$,
故答案为:1,2.
点评 本替考查分式的加减法、解二元一次方程组,解答本题的关键是明确它们各自的计算方法.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:选择题
| A. | (-1,5) | B. | (0,5) | C. | (9,5) | D. | (-1,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
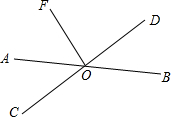 如图,直线AB、CD相交于点O,OF⊥CO,∠AOF与∠BOD的度数之比为3:2,则∠AOC的度数是( )
如图,直线AB、CD相交于点O,OF⊥CO,∠AOF与∠BOD的度数之比为3:2,则∠AOC的度数是( )| A. | 18° | B. | 45° | C. | 36° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{13}$ | B. | 3$\sqrt{2}$ | C. | 5 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
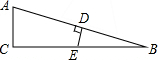 如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交AB于D,交BC于E,若BE=8cm,则AC的长为( )
如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交AB于D,交BC于E,若BE=8cm,则AC的长为( )| A. | 4cm | B. | 5cm | C. | 6cm | D. | 8cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
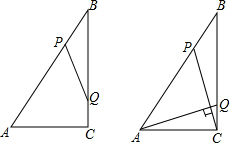 如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com