
【题目】如图,已知二次函数![]() 的图象与x轴交于A,B两点与y轴交于点C,⊙C的半径为
的图象与x轴交于A,B两点与y轴交于点C,⊙C的半径为![]() ,P为⊙C上一动点.
,P为⊙C上一动点.
(1)点B,C的坐标分别为B( ),C( );
(2)当P点运动到(-1,-2)时,判断PB与⊙C的位置关系,并说出理由;
(3)是否存在点P,使得△PBC是以BC为斜边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(4)连接PB,若E为PB的中点,连接OE,则OE的最大值= .
【答案】(1)B(3,0),C(0,-4);(2)相切,理由详见解析;(3)存在,P1(-1,-2)或P2(![]() ,
,![]() );(4)
);(4)![]()
【解析】
(1)在抛物线中令y=0即可求出点B的坐标,令x=0即可求出点C的坐标;
(2)分别求出三边的长度即可得出答案;
(3)根据勾股定理求出BC和![]() 的长度,过
的长度,过![]() 作
作![]() ⊥x轴于点E,
⊥x轴于点E,![]() ⊥y轴于点F,根据相似三角形的性质得出
⊥y轴于点F,根据相似三角形的性质得出![]() ,设
,设![]() ,
,![]() 即可得出BE和CF的长度,解出x的值即可得出P2的坐标,同理即可得出P1的坐标;
即可得出BE和CF的长度,解出x的值即可得出P2的坐标,同理即可得出P1的坐标;
(4)根据中位线定理AP最大时,OE的值最大.
解:(1)在![]() 中,令 y=0, 则x=3 或-3,令 x=0, 则y=-4
中,令 y=0, 则x=3 或-3,令 x=0, 则y=-4
故B(3,0),C(0,-4);
(2)当P点运动到(-1,-2)时,PB与⊙C相切;
此时PB2=20,PC2=5,BC2=25,可得PB2+PC2=BC2,
从而CP⊥PB,∴PB与⊙C相切.
(3)存在点P,使得△PBC为直角三角形.
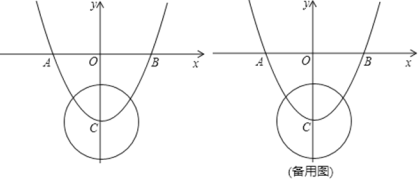
①当PB与圆O相切时,△PBC是直角三角形,如图,连接BC
∵OB=3,OC=4
∴BC=5
∵![]() ,
,![]()
∴![]()
过![]() 作
作![]() ⊥x轴于点E,
⊥x轴于点E,![]() ⊥y轴于点F
⊥y轴于点F
则△![]() ∽△
∽△![]() ,四边形
,四边形![]() 是矩形
是矩形
∴![]()
设![]() ,
,![]()
∴BE=3-x,CF=2x-4
∴![]()
解得:![]()
∴![]() ,
,![]()
∴P2(![]() ,
,![]() )
)
②同理求得:P1(-1,-2)
综上所述,点P的坐标为:P1(-1,-2)或P2(![]() ,
,![]() );
);
(4)![]()
如图∵E为PB的中点,OE是△BAP的中位线
∴OE=![]() AP
AP
∵![]()
∴![]()


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
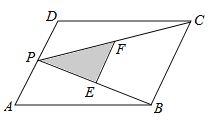
【题目】如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,![]() ,
,![]() .若S=3,则
.若S=3,则![]() 的值为( )
的值为( )
A.24B.12C.6D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明研究一函数的性质,下表是该函数的几组对应值:
| ··· | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | ···· |
| ··· | 8 | 3 | 0 | -1 | 0 | 3 | 0 | -3 | -6 | ···· |
![]() 在平面直角坐标系中,描出以上表格中的各点,根据描出的点,画出该函数图象
在平面直角坐标系中,描出以上表格中的各点,根据描出的点,画出该函数图象
![]() 根据所画函数图象,写出该函数的一条性质: ;
根据所画函数图象,写出该函数的一条性质: ;
![]() 根据图像直接写出该函数的解析式及自变量的取值范围: ;
根据图像直接写出该函数的解析式及自变量的取值范围: ;
![]() 若一次函数
若一次函数![]() 与该函数图像有三个交点,则
与该函数图像有三个交点,则![]() 的范围是
的范围是

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商城经销甲、乙两种商品,甲种商品每件进价12元,售价20元;乙种商品每件进价28元,
售价40元.商城用2288元购进了甲、乙两种商品共100件.
(1)求购进甲、乙两种商品各多少件?
(2)若商城对商品的售价进行调整,甲种商品在原售价的基础上上调![]() (a大于0)出售,乙种商品在原售价基础上下调1.5
(a大于0)出售,乙种商品在原售价基础上下调1.5![]() 出售.为保障商城在销售这100件商品所获得的利润不低于728无,求a的最大值.
出售.为保障商城在销售这100件商品所获得的利润不低于728无,求a的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某市药监部门为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调査.
(1)下列选取样本的方法最合理的一种是 .(只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;②在全市医务工作者中以家庭为单位随机抽取;③在全市常住人口中以家庭为单位随机抽取.
(2)本次抽样调査发现,接受调査的家庭都有过期药品,现将有关数据呈现如图:
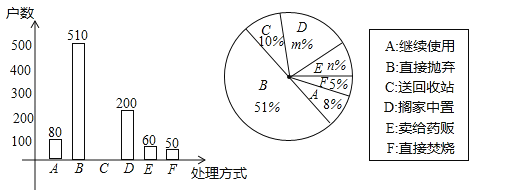
①m= ,n= ;
②补全条形统计图;
③根据调査数据,你认为该市市民家庭处理过期药品最常见的方式是什么?
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育锻炼对学生的健康成长有着深远的影响.某中学 开展了四项球类活动:A:乒乓球;B:足球;C:排球;D:篮球.王老师对学生最喜欢的一项球类活动进行了抽样调查(每人只限一项),并将调查结果绘制成图 1,图2两幅不完整的统计图.
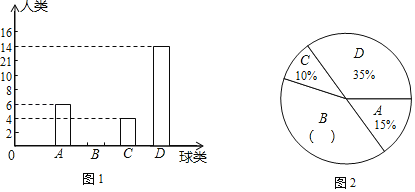
请根据图中信息解答下列问题:
(1)参加此次调查的学生总数是 人;将图1、图2的统计图补充完整;
(2)已知在被调查的最喜欢排球项目的4名学生中只有1名女生,现从这4名学生中任意抽取2名学生参加校排球队,请用列表法或画树状图的方法,求出恰好抽到一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西安市某学校在“我们如何预防感染新型冠状病毒”宣讲培训后,对学生知晓情况进行了一次测试,其测试成绩按照标准划分为四个等级:![]() 优秀,
优秀,![]() 良好,
良好,![]() 合格,
合格,![]() 不合格.为了了解该校学生的成绩状况,对在校学生进行随机抽样调查,并对调查结果进行统计,如图所示.
不合格.为了了解该校学生的成绩状况,对在校学生进行随机抽样调查,并对调查结果进行统计,如图所示.
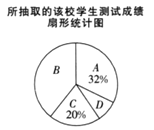

请结合统计图回答下列问题:
(1)该校抽样调查的学生人数为___________.
(2)请补全条形统计图.
(3)样本中,学生成绩的中位数所在等级是______.(填“![]() ”、“
”、“![]() ”、“
”、“![]() ”或“
”或“![]() ”)
”)
(4)该校共有学生2500人,估计全校测试成绩为优秀和良好的学生共有______人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在江苏省某林场东西方向的两地之间修一条公路MN,已知C点周围200米范围内为原始森林保护区,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走600米到达B处,测得C在点B的北偏西60°方向上.

(1)MN是否穿过原始森林保护区?为什么?(参考数据:![]() )
)
(2)若修路工程工程需尽快完成.如果由甲、乙两个工程队合做,12天可完成;如果由甲、乙两队单独做,甲队比乙队少用10天完成.求甲、乙两工程队单独完成此项工程所需的天数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com