
【题目】如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1 , y2(千米)与行驶时间x(小时)之间的函数关系图象.
(1)填空:A,B两地相距千米;
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;
(3)当客车行驶多长时间,客、货两车相距150千米.
【答案】
(1)420
(2)解:设两小时后,货车离C站的路程y与行驶时间x之间的函数关系式是y =kx+b,
由图象可知,货车的速度为:60÷2=30千米/时,
∴货车到达A的时间为:420÷30=14(小时),
∴点P的坐标为(14,360),
∴ ![]() ,得
,得 ![]() ,
,
即两小时后,货车离C站的路程y 与行驶时间x之间的函数关系式是y =30x60
(3)解:由题意可得,
(420150)×(60÷2+360÷6)=3(小时),
当客车行驶3小时时,客、货两车相距150千米。
【解析】(1)由函数图象可得,
A,B两地相距:60+360=420(千米),
所以答案是:420;
【考点精析】本题主要考查了一次函数的图象和性质的相关知识点,需要掌握一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】下列说法:①全等图形的形状相同、大小相等;②全等三角形的对应边相等;③全等三角形的周长、面积分别相等;④面积相等的两个三角形全等,其中正确的说法为( )
A. ①③④ B. ②③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=﹣ ![]() x+2和y=2x﹣3的图象分别交y轴与A、B两点,两个一次函数的图象相交于点P.
x+2和y=2x﹣3的图象分别交y轴与A、B两点,两个一次函数的图象相交于点P.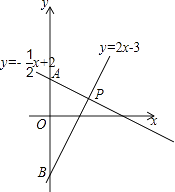
(1)求△PAB的面积;
(2)求证:∠APB=90°;
(3)若在一次函数y=2x﹣3的图象上有一点N,且横坐标为x,连结NA,请直接写出△NAP的面积关于x的函数关系式,并写出相应x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1 , 第二次将△QA1B1变换成△OA2B2 , 第三次将△OA2B2变换成△OA3B3 . 已知A(1,3),A1(2,3),A2(4,3),A3(8,3);B(2,0),B1(4,0),B2(8,0),B3(16,0)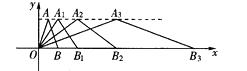
(1)观察每次变换前后三角形的变化规律,若再将△OA3B3变换成△OA4B4 , 则点A4的坐标为 , 点B4的坐标为;
(2)若按第(1)题找到的规律将△OAB进行n次变换,得到△OAnBn , 则点An的坐标为 , 点Bn的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
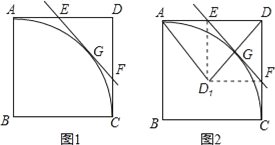
【题目】如图1所示,在正方形ABCD中,AB=1, ![]() 是以点B为圆心,AB长为半径的圆的一段弧,点E是边AD上的动点(点E与点A,D不重合),过E作
是以点B为圆心,AB长为半径的圆的一段弧,点E是边AD上的动点(点E与点A,D不重合),过E作![]() 所在圆的切线,交边DC于点F,G为切点.
所在圆的切线,交边DC于点F,G为切点.
(1)求证:EA=EG;
(2)设AE=x,FC=y,求y关于x的函数关系式,并直接写出x的取值范围;
(3)如图2所示,将△DEF沿直线EF翻折后得△D1EF,连接AD1,D1D,试探索:当点E运动到何处时,△AD1D与△ED1F相似?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30﹣40含起点值30,不含终点值40),得到其频数及频率如表: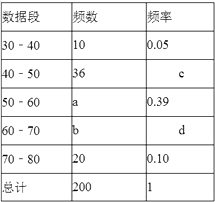
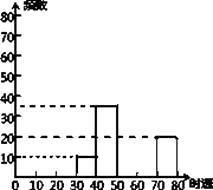
(1)表中a、b、c、d分别为:a=; b=; c=; d=.
(2)补全频数分布直方图;
(3)如果某天该路段约有1500辆通过,汽车时速不低于60千米即为违章,通过该统计数据估计当天违章车辆约有多少辆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com