
【题目】某中学计划从办公用品公司购买A,B两种型号的小黑板.经洽谈,购买一块A型小黑板比购买一块B型小黑板多用20元,且购买5块A型小黑板和4块B型小黑板共需820元.
(1)求购买一块A型小黑板、一块B型小黑板各需多少元.
(2)根据该中学实际情况,需从公司购买A,B两种型号的小黑板共60块,要求购买A,B两种型号小黑板的总费用不超过5240元.并且购买A型小黑板的数量不小于购买B型小黑板数量的 ![]() .则该中学从公司购买A,B两种型号的小黑板有哪几种方案?哪种方案的总费用最低?
.则该中学从公司购买A,B两种型号的小黑板有哪几种方案?哪种方案的总费用最低?
【答案】
(1)解:设一块A型小黑板x元,一块B型小黑板y元.
则 ![]() ,
,
解得 ![]() .
.
答:一块A型小黑板100元,一块B型小黑板80元
(2)解:设购买A型小黑板m块,则购买B型小黑板(60﹣m)块
则 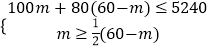 ,
,
解得20≤m≤22,
又∵m为正整数
∴m=20,21,22
则相应的60﹣m=40,39,38
∴共有三种购买方案,分别是
方案一:购买A型小黑板20块,购买B型小黑板40块;
方案二:购买A型小黑板21块,购买B型小黑板39块;
方案三:购买A型小黑板22块,购买B型小黑板38块.
方案一费用为100×20+80×40=5200元;
方案二费用为100×21+80×39=5220元;
方案三费用为100×22+80×38=5240元.
∴方案一的总费用最低,
即购买A型小黑板20块,购买B型小黑板40块总费用最低,为5200元
【解析】(1)设购买一块A型小黑板需要x元,一块B型为y元,根据等量关系:购买一块A型小黑板比买一块B型小黑板多用20元;购买5块A型小黑板和4块B型小黑板共需820元;可列方程组求解.(2)设购买A型小黑板m块,则购买B型小黑板(60﹣m)块,根据需从公司购买A、B两种型号的小黑板共60块,要求购买A、B两种型号小黑板的总费用不超过5240元.并且购买A型小黑板的数量不小于购买B型小黑板数量的 ![]() ,可列不等式组求解.
,可列不等式组求解.
【考点精析】关于本题考查的一元一次不等式组的应用,需要了解1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知,BC∥OA,∠B=∠A=100°,试回答下列问题: 
(1)如图①,求证:OB∥AC.
(2)如图②,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.则∠EOC的度数等于;(在横线上填上答案即可).
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.
(4)在(3)的条件下,如果平行移动AC的过程中,若使∠OEB=∠OCA,此时∠OCA度数等于 . (在横线上填上答案即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解1000个箱子的质量情况,从中随机抽取50个箱子进行检查,则抽样( )
A. 不够合理,容量太小B. 不够合理,不具有代表性
C. 不够合理,遗漏了950个箱子D. 合理、科学
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列因式分解正确的是( )
A. 2x2-2=2(x+1)(x-1) B. x2+2x-1=(x-1)2
C. x2+1=(x+1)2 D. x2-x+2=x(x-1)+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于2300+(-2)301的计算结果正确的是( )
A. 2300+(-2)301=(-2)300+(-2)301=(-2)601 B. 2300+(-2)301=2300-2301=2-1
C. 2300+(-2)301=2300-2301=2300-2×2300=-2300 D. 2300+(-2)301=2300+2301=2601
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com