
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | c<b<a |
分析 先计算对称轴为直线x=$\frac{1}{2}$,抛物线开口向下,可知A点为顶点(最高点),a最大;再根据B、C两点与对称轴的远近,比较纵坐标的大小.
解答 解:抛物线y=-x2+x+3的对称轴是直线x=$\frac{1}{2}$,开口向下,
点A($\frac{1}{2}$,a)为顶点,即最高点,
所以,a最大,A、B错误;
又1<sin30°+cos30°<2,-m2+2m-2=-(m-1)2-1≤-1,
可知,B点离对称轴近,C点离对称轴远,
由于抛物线开口向下,
离对称轴越远,函数值越小,c<b,C错误;
故选D.
点评 本题考查了二次函数图象上点的坐标特征,二次函数的性质,熟练掌握二次函数的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
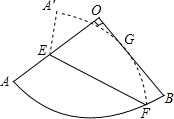 如图,已知扇形AOB的半径为6,圆心角为90°,E是半径OA上一点,F是$\widehat{AB}$上一点.将扇形AOB沿EF对折,使得折叠后的圆弧$\widehat{A'F}$恰好与半径OB相切于点G.若OE=4,则O到折痕EF的距离为2$\sqrt{3}$.
如图,已知扇形AOB的半径为6,圆心角为90°,E是半径OA上一点,F是$\widehat{AB}$上一点.将扇形AOB沿EF对折,使得折叠后的圆弧$\widehat{A'F}$恰好与半径OB相切于点G.若OE=4,则O到折痕EF的距离为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
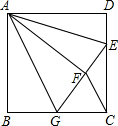 如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.下列结论:①点G是BC中点;②FG=FC;③与∠AGB相等的角有5个;④S△FGC=$\frac{9}{10}$.其中正确的有①④.
如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.下列结论:①点G是BC中点;②FG=FC;③与∠AGB相等的角有5个;④S△FGC=$\frac{9}{10}$.其中正确的有①④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
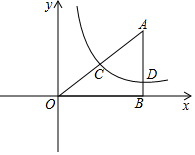 如图,Rt△ABO在直角坐标系中,AB⊥x轴于点B,AO=10,sin∠AOB=$\frac{3}{5}$.
如图,Rt△ABO在直角坐标系中,AB⊥x轴于点B,AO=10,sin∠AOB=$\frac{3}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
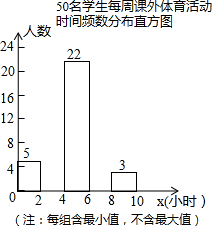 为了解学生每周课外体育活动时间的情况,某学校随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%,根据以上信息及统计图解答下列问题:
为了解学生每周课外体育活动时间的情况,某学校随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%,根据以上信息及统计图解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com