
【题目】小明用a小时清点完一批图书的一半,小强加入清点另一半图书的工作,两人合作![]() 小时清点完另一半图书.设小强单独清点完这批图书需要x小时.
小时清点完另一半图书.设小强单独清点完这批图书需要x小时.
(1)若a=3,求小强单独清点完这批图书需要的时间.
(2)请用含a的代数式表示x,并说明a满足什么条件时x的值符合实际意义.
【答案】解:(1)设小强单独清点完这批图书需要x小时,由题意得:![]() +(
+(![]() +
+![]() )×
)×![]() =1,
=1,
解得:x=4,
经检验x=4是原分式方程的解.
答:小强单独清点完这批图书需要4小时.
(2)由题意得:![]() +(
+(![]() +
+![]() )×
)×![]() =1,
=1,
解得:x=![]() ,
,
a>![]() .
.
所以当a>![]() 时x的值符合实际意义.
时x的值符合实际意义.
【解析】(1)设小强单独清点这批图书需要的时间是x小时,根据“小明3小时清点完一批图书的一半”和“两人合作![]() 小时清点完另一半图书”列出方程,求出x的值,再进行检验,即可得出答案;
小时清点完另一半图书”列出方程,求出x的值,再进行检验,即可得出答案;
(2)根据小明完成的工作量加上两人合作完成的工作量为1,列出方程解答即可.
【考点精析】本题主要考查了分式方程的应用的相关知识点,需要掌握列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】
如图,以![]() 为直径的⊙O交△CFB的边
为直径的⊙O交△CFB的边![]() 于点A,
于点A, ![]() 平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF·AC。
平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF·AC。
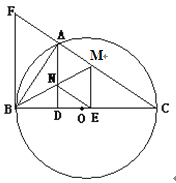
(1)证明:△ABM≌△EBM;
(2)证明:FB是⊙O的切线;
(3)若cos∠ABD=![]() ,AD=12.求四边形AMEN的面积S。
,AD=12.求四边形AMEN的面积S。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AM、BN分别与⊙O相切于点A、B,CD交AM、BN于点D、C,DO平分∠ADC.
(1)求证:CD是⊙O的切线;
(2)设AD=4,AB=x (x > 0),BC=y (y > 0). 求y关于x的函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在4×4的网格中存在线段AB,每格表示一个单位长度,并构建了平面直角坐标系.
(1)直接写出点A、B的坐标:A( ,),B( ,);
(2)请在图中确定点C(1,﹣2)的位置并连接AC、BC,则△ABC是三角形(判断其形状);
(3)在现在的网格中(包括网格的边界)存在一点P,点P的横纵坐标为整数,连接PA、PB后得到△PAB为等腰三角形,则满足条件的点P有个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】明天下雨的概率为95%,那么下列说法错误的是( )
A. 明天下雨的可能性较大
B. 明天不下雨的可能性较小
C. 明天有可能是晴天
D. 明天不可能是晴天
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下面例题,解答问题:
例题:已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得
x2﹣4x+m=(x+3)(x+n)
则x2﹣4x+m=x2+(n+3)x+3n
∴![]() .
.
解得:n=﹣7,m=﹣21
∴另一个因式为(x﹣7),m的值为﹣21
问题:仿照以上方法解答下面问题:
已知二次三项式2x2+3x﹣k有一个因式是(2x﹣5),求另一个因式以及k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点A对应的数为a,点B对应的数为b,且多项式x3y﹣2xy+5的二次项系数为a,常数项为b.
(1)直接写出:a= , b= .
(2)数轴上点A、B之间有一点动P,若点P对应的数为x,试化简|2x+4|+2|x﹣5|﹣|6﹣x|;
(3)若点M从点A出发,以每秒1个单位长度的速度沿数轴向右移动:同时点N从点B出发,沿数轴以每秒2个单位长度的速度向左移动,到达A点后立即返回并向右继续移动,请直接写出经过秒后,M、N两点相距1个单位长度,并选择一种情况计算说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com