
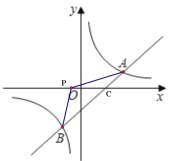
【题目】如图,反比例函数y=![]() 与一次函数y=ax+b交于A(3,1)和B(1,m)两点.
与一次函数y=ax+b交于A(3,1)和B(1,m)两点.

(1)求一次函数和反比例函数的解析式;
(2)结合函数图象,请直接写出![]() >ax+b的解集;
>ax+b的解集;
(3)若P是x轴上一点,且△ABP的面积是6,求点P的坐标.
【答案】(1)y=![]() ,y=x2;(2)x<1或0<x<3;(3)P点(-1,0)或(5,0)
,y=x2;(2)x<1或0<x<3;(3)P点(-1,0)或(5,0)
【解析】
(1)先由点A(3,1)确定k的值,即可确定反比例函数解析式,再确定B点坐标,然后用待定系数法即可确定B点坐标;
(2)根据函数图像可直接确定答案;
(3)设P点坐标为(a,0),再求出C点坐标(0,2),则OC=|a-2|,则△ACP边OC上的高为1,△BCP边OC上的高为3;最后根据S△ABP=S△ACP+S△BCP=6即可解答.
解:(1)∵点A(3,1)在反比例函数y=![]() 的图像上,
的图像上,
∴k=3×1=3,
∴反比例函数的表达式为y=![]() ,
,
∵点B(1,m)也在反比例函数y=![]() 的图像上,
的图像上,
∴m=![]() =3,即B(1,3),
=3,即B(1,3),
把点A(3,1),点B(1,3)代入一次函数y=ax+b中,
得![]() ,解得
,解得![]() ,
,
∴一次函数的表达式为y=x2;
(2)观察图象可得:x<1或0<x<3.
(3)如图:设P点坐标为(a,0)
∵C为直线AB于x轴交点
∴C(2,0)
∴OC=|a-2|
∵△ACP边OC上的高为1,△BCP边OC上的高为3, △ABP的面积是6
∴S△ABP=S△ACP+S△BCP=6,即![]()
解得a=-1或a=5
∴P点(-1,0)或(5,0)


科目:初中数学 来源: 题型:
【题目】已知一个函数y与自变量x的部分对应值如下表:

(1)从我们已学过的函数判断:y是x的 函数,y与x的函数关系式为 ;
(2)根据函数图像,当-2 x -![]() 时,求y的取值范围.
时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠A=90°+x°,∠B=90°﹣x°,∠CED=90°,4∠C﹣∠D=30°,射线EF∥AC.
(1)判断射线EF与BD的位置关系,并说明理由;
(2)求∠C,∠D的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个不透明口袋,装有分别标有数字1,2,3,4的4个小球(小球除数字不同外,其余都相同),另有3张背面完全一样、正面分别写有数字1,2,3的卡片.小敏从口袋中任意摸出一个小球,小颖从这3张背面朝上的卡片中任意摸出一张,然后计算小球和卡片上的两个数的积.
(1)请你用列表或画树状图的方法,求摸出的这两个数的积为6的概率;
(2)小敏和小颖做游戏,她们约定:若这两个数的积为奇数,小敏赢;否则,小颖赢.你认为该游戏公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划组织![]() 名师生租乘汽车外出研学一天,需租用大巴、中巴共
名师生租乘汽车外出研学一天,需租用大巴、中巴共![]() 辆,且要求租用的车子不留空位也不超载,大巴每辆可乘坐
辆,且要求租用的车子不留空位也不超载,大巴每辆可乘坐![]() 名乘客,中巴每辆可乘坐
名乘客,中巴每辆可乘坐![]() 名乘客.
名乘客.
(1)求该校应租用大巴、中巴各多少辆?(请用含![]() 的代数式表示)
的代数式表示)
(2)若每辆大巴租金是![]() 元/天,中巴租金是
元/天,中巴租金是![]() 元/天,若租金不能超过
元/天,若租金不能超过![]() 元,则应租用大巴、中巴各多少辆?
元,则应租用大巴、中巴各多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC中∠ BAC的外角平分线,BD⊥AD于D,E为BC中点,DE=5,AC=3,则AB长为()

A.8.5B.8C.7.5D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
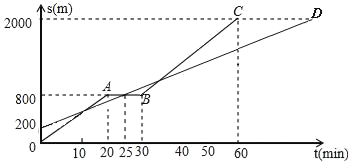
【题目】小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发匀速前行,且途中休息一段时间后继续以原速前行.家到公园的距离为2000m,如图是小明和爸爸所走的路程S(m)与步行时间t(min)的函数图象.
(1)直接写出BC段图象所对应的函数关系式(不用写出t的取值范围).
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早18分钟到达公园,则小明在步行过程中停留的时间需减少 分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个木制正方体的表面涂上颜色,然后将正方形分割成27个大小相同的小正方体,从这些小正方体中任意取出一个,求取出的小正方体;
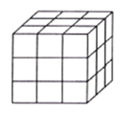
(1)只有一面涂有颜色的概率;
(2)至少有两面涂有颜色的概率;
(3)各个面都没有颜色的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com