
【题目】如图,在△ABC中,BE、CE 分别是∠ABC 和∠ACB 的平分线,过点 E 作 DF∥BC,交 AB 于 D,交 AC 于 F,若 AB=5,AC=4,则△ADF周长为________.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】定义:若点P为四边形ABCD内一点,且满足∠APB+∠CPD=180°, 则称点P为四边形ABCD的一个“互补点”.
(1)如图1,点P为四边形ABCD的一个“互补点”,∠APD=63°,求∠BPC的度数.

(2)如图2,点P是菱形ABCD对角线上的任意一点.求证:点P为菱形ABCD的一个“互补点”.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建设银行的某储蓄员小张在办理业务时,约定存入为正,取出为负. 2019年10月29日,他先后办理了七笔业务: +2000元、-800元、+400元、-800元、+1400元、-1700元、-200元.
(1)若他早上领取备用金4000元,那么下班时应交回银行_________元钱.
(2)请判断在这七次办理业务中,小张在第_______次业务办理后手中现金最多,第_________次业务办理后手中现金最少.
(3)若每办一件业务,银行发给业务量的0.2%作为奖励,小张这天应得奖金多少元?
(4)若记小张第一次办理业务前的现金为0点,用折线统计图表示这7次业务办理中小张手中现金的变化情况.
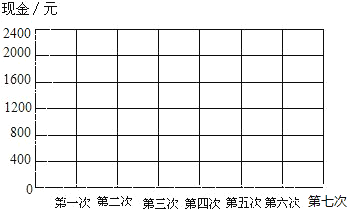
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某博物馆的票价是:成人票![]() 元,学生票
元,学生票![]() 元,满
元,满![]() 人可以购买团体票(不足
人可以购买团体票(不足![]() 人可按
人可按![]() 人计算,票价打
人计算,票价打![]() 折),某班在
折),某班在![]() 位老师带领下去博物馆,学生人数为
位老师带领下去博物馆,学生人数为![]() 人.
人.
![]() 如果学生人数大于
如果学生人数大于![]() 人,该班买票至少应付 元.(用含
人,该班买票至少应付 元.(用含 ![]() 的代数式表示)
的代数式表示)
![]() 如果学生人数小于
如果学生人数小于![]() 人,该班买票至少应付 元.(用含
人,该班买票至少应付 元.(用含![]() 的代数式表示)
的代数式表示)
![]() 如果学生人数为
如果学生人数为![]() 人,该班买票至少应付多少元?
人,该班买票至少应付多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:abc<0;②9a+3b+c>0;③若点M(![]() ,y1),点N(
,y1),点N(![]() ,y2)是函数图象上的两点,则y1<y2;④﹣
,y2)是函数图象上的两点,则y1<y2;④﹣![]() <a<﹣
<a<﹣![]() .其中正确结论有( )
.其中正确结论有( )
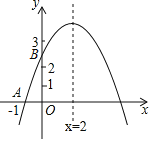
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请把下列证明过程补充完整.已知:如图,B、C、E三点在同一直线上,A、F、E三点在同一直线上,∠1=∠2=∠E,∠3=∠4.求证:AB∥CD.
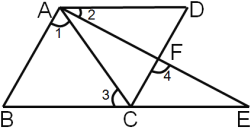
证明:∵∠2=∠E(已知)
∴ ∥BC( )
∴∠3=∠ ( )
∵∠3=∠4(已知)
∴∠4=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF ,即∠BAF=∠
∴∠4=∠ (等量代换)
∴ ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列结论:①若![]() ,则
,则![]() 互为相反数;②若
互为相反数;②若![]() ,则
,则![]() 且
且![]() ;③
;③![]() ;④绝对值小于10的所有整数之和等于0;⑤3与-5是同类项.其中正确的结论有( )个.
;④绝对值小于10的所有整数之和等于0;⑤3与-5是同类项.其中正确的结论有( )个.
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若两个三角形,有两边相等且其中一组等边所对的角对应相等,但不是全等三角形,我们就称这两个三角形为偏差三角形.
(1)如图1,已知A(3,2),B(4,0),请在x轴上找一个C,使得△OAB与△OAC是偏差三角形.你找到的C点的坐标是______,直接写出∠OBA和∠OCA的数量关系______.
(2)如图2,在四边形ABCD中,AC平分∠BAD,∠D+∠B=180°,问△ABC与△ACD是偏差三角形吗?请说明理由.
(3)如图3,在四边形ABCD中,AB=DC,AC与BD交于点P,BD+AC=9,∠BAC+∠BDC=180°,其中∠BDC<90°,且点C到直线BD的距离是3,求△ABC与△BCD的面积之和.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com