
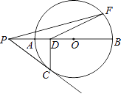
【题目】如图,⊙O中,PC切⊙O于点C,连PO交于⊙O点A、B,点F是⊙O上一点,连PF,CD⊥AB于点D,AD=2,CD=4,则PF:DF的值是( )
A. 2 B. ![]() C. 5:3 D. 4:3
C. 5:3 D. 4:3
【答案】C
【解析】
连接AC、OC、OF、BC.由△ADC∽△CDB,推出![]() ,求出DB、OA、OD,由△ODC∽△OCP,推出
,求出DB、OA、OD,由△ODC∽△OCP,推出![]() ,推出OC2=ODOP,推出OF2=ODOP,即
,推出OC2=ODOP,推出OF2=ODOP,即![]() ,由∠DOF=∠POF,推出△DOF∽△FOP,可得
,由∠DOF=∠POF,推出△DOF∽△FOP,可得![]() .
.
连接AC、OC、OF、BC.如图所示:
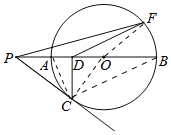
∵AB是直径,
∴∠ACB=90°,
∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠ACD+∠CAD=90°,∠ACD+∠BCD=90°,
∴∠CAD=∠BCD,
∴△ADC∽△CDB,
∴![]() ,
,
∴![]() ,
,
∴DB=8,OA=OB=5,OD=3,
∵PC是切线,
∴OC⊥PC,
∵∠DOC=∠POC,∠ODC=∠OCP,
∴△ODC∽△OCP,
∴![]() ,
,
∴OC2=ODOP,
∴OF2=ODOP,
∴![]() ,
,
∵∠DOF=∠POF,
∴△DOF∽△FOP,
∴![]() ,
,
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
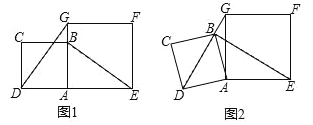
【题目】正方形ABCD和正方形AEFG的边长分别为2和![]() ,点B在边AG上,点D在线段EA的延长线上,连接BE.
,点B在边AG上,点D在线段EA的延长线上,连接BE.
(1)如图1,求证:DG⊥BE;
(2)如图2,将正方形ABCD绕点A按逆时针方向旋转,当点B恰好落在线段DG上时,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=![]() ,求
,求![]() 的值.
的值.
(3)(3分)在(2)的条件下,设⊙O的半径为3,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“共建环保模范城,共享绿色新重庆”,市政府强力推进城市生活污水处理、生活垃圾处理设施建设改造工作.为此,某化工厂在一期工程完成后购买了4台甲型和5台乙型污水处理设备,共花费资金102万元,且每台乙型设备的价格比每台甲型设备价格少3万元.已知每台甲型设备每月能处理污水240吨,每台乙型设备每月能处理污水180吨.今年该厂二期工程即将完成,产生的污水将大大增加,于是该厂决定再购买甲、乙两型设备共12台用于二期工程的污水处理,预算本次购买资金不超过129万元,预计二期工程完成后每月将产生不少于2220吨污水.
(1)请你计算每台甲型设备和每台乙型设备的价格各是多少万元?
(2)请你求出用于二期工程的污水处理设备的所有购买方案;
(3)请你说明在(2)的所有方案中,哪种购买方案的总花费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
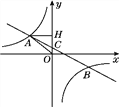
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=![]() ,点B的坐标为(m,-2).
,点B的坐标为(m,-2).
(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
【答案】(1)△AHO的周长为12;(2) 反比例函数的解析式为y=![]() ,一次函数的解析式为y=-
,一次函数的解析式为y=-![]() x+1.
x+1.
【解析】试题分析: (1)根据正切函数,可得AH的长,根据勾股定理,可得AO的长,根据三角形的周长,可得答案;
(2)根据待定系数法,可得函数解析式.
试题解析:(1)由OH=3,tan∠AOH=![]() ,得
,得
AH=4.即A(-4,3).
由勾股定理,得
AO=![]() =5,
=5,
△AHO的周长=AO+AH+OH=3+4+5=12;
(2)将A点坐标代入y=![]() (k≠0),得
(k≠0),得
k=-4×3=-12,
反比例函数的解析式为y=![]() ;
;
当y=-2时,-2=![]() ,解得x=6,即B(6,-2).
,解得x=6,即B(6,-2).
将A、B点坐标代入y=ax+b,得
![]() ,
,
解得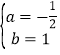 ,
,
一次函数的解析式为y=-![]() x+1.
x+1.
考点:反比例函数与一次函数的交点问题.
【题型】解答题
【结束】
21
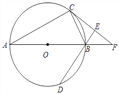
【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB交DB的延长线于点E,直线AB与CE相交于点F.
(1)求证:CF为⊙O的切线;
(2)填空:当∠CAB的度数为________时,四边形ACFD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
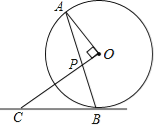
【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为![]() ,OP=1,求BC的长.
,OP=1,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A在反比例函数y=![]() (x>0)的图象上,作Rt△ABC,边BC在x轴上,点D为斜边AC的中点,连结DB并延长交y轴于点E,若△BCE的面积为4,则k的值是( )
(x>0)的图象上,作Rt△ABC,边BC在x轴上,点D为斜边AC的中点,连结DB并延长交y轴于点E,若△BCE的面积为4,则k的值是( )
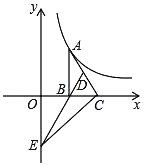
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() 为正方形
为正方形![]() 的中心,分别延长
的中心,分别延长![]() 到点
到点![]() ,
, ![]() 到点
到点![]() ,使
,使![]() ,
, ![]() ,连结
,连结![]() ,将△
,将△![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 角得到△
角得到△![]() (如图2).连结
(如图2).连结![]() 、
、![]() .
.
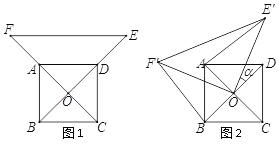
(Ⅰ)探究![]() 与
与![]() 的数量关系,并给予证明;
的数量关系,并给予证明;
(Ⅱ)当![]() ,
, ![]() 时,求:
时,求:
①![]() 的度数;
的度数;
②![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com