
【题目】综合与实践:矩形的旋转
问题情境:
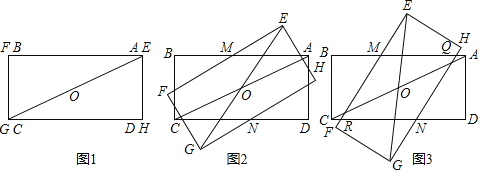
在综合与实践课上,老师让同学们以“矩形的旋转”为主题开展数学活动.具体要求:如图1,将长与宽都相等的两个矩形纸片ABCD和EFGH叠放在一起,这时对角线AC和EG互相重合.固定矩形ABCD,将矩形EFGH绕AC的中点O逆时针方向旋转,直到点E与点B重合时停止,在此过程中开展探究活动.
操作发现:
(1)雄鹰小组初步发现:在旋转过程中,当边AB与EF交于点M,边CD与GH交于点N,如图2、图3所示,则线段AM与CN始终存在的数量关系是 .
(2)雄鹰小组继续探究发现:在旋转开始后,当两个矩形纸片重叠部分为四边形QMRN时,如图3所示,四边形QMRN为菱形,请你证明这个结论.
(3)雄鹰小组还发现在问题(2)中的四边形QMRN中∠MQN与旋转角∠AOE存在着特定的数量关系,请你写出这一关系,并说明理由.
实践探究:
(4)在图3中,随着矩形纸片EFGH的旋转,四边形QMRN的面积会发生变化.若矩形纸片的长为![]() ,宽为
,宽为![]() ,请你帮助雄鹰小组探究当旋转角∠AOE为多少度时,四边形QMRN的面积最大?最大面积是多少?(直接写出答案)
,请你帮助雄鹰小组探究当旋转角∠AOE为多少度时,四边形QMRN的面积最大?最大面积是多少?(直接写出答案)
【答案】(1)结论:AM=CN,理由见解析;
(2)证明见解析;
(3)结论:∠MQN=∠AOE,理由见解析;
(4)∠AOE=45°或135°时,四边形QMRN面积最大为![]() .
.
【解析】
(1)先证明△AOK≌△AOJ(ASA),推出OK=OJ,AK=CJ,∠AOK=∠AJO,再证明△EKM≌△GJN(ASA)即可的解;(2)过点Q作QK⊥EF,QL⊥CD,垂足分别为点K,L、先证明四边形QMRN是平行四边形,再证明QM=QN即可的解;(3)由三角形的外角的性质以及平行线的性质即可解决问题;(4)如图3-2中,连接BD,在DC上取一点J,使得DJ=AD=![]() ,则AJ=2,通过解直角三角形求出∠BOC的度数,再结合图象即可得解.
,则AJ=2,通过解直角三角形求出∠BOC的度数,再结合图象即可得解.
(1)结论:AM=CN.
理由:如图2中,设AB交EG于K,CD交EG于J.
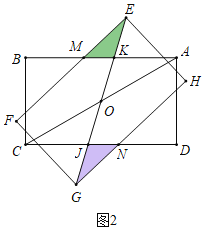
∵四边形ABCD是矩形,四边形EFGH是矩形,
∴AB∥CD,EF∥EG,OA=OC=OE=OG,
∴∠MEK=∠JGN,∠OAK=∠OAJ,
∵∠AOK=∠AOJ,∴△AOK≌△AOJ(ASA),
∴OK=OJ,AK=CJ,∠AOK=∠AJO,∴EK=JG,
∵∠EKM=∠AKO,∠GJN=∠CJO,∴∠EKM=∠GJN,
∴△EKM≌△GJN(ASA),∴KM=JN,∴AM=AN.
(2)证明:过点Q作QK⊥EF,QL⊥CD,垂足分别为点K,L.
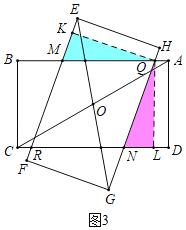
由题可知:矩形ABCD≌矩形EFGH,
∴AD=EH,AB∥CD,EF∥HG,
∴四边形QMRN为平行四边形,
∵QK⊥EF,QL⊥CD,∴QK=EH,QL=AD,∠QKM=∠QLN=90°,∴QK=QL,
又∵AB∥CD,EF∥HG,∴∠KMQ=∠MQN,∠MQN=∠LNQ,
∴∠KMQ=∠LNQ,∴△QKM≌△QLN(AAS),
∴MQ=NQ∴四边形QMRN为菱形.
(3)结论:∠MQN=∠AOE.理由:如图3﹣1中,
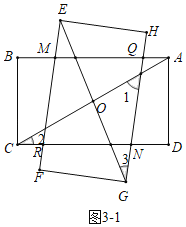
∵∠QND=∠1+∠2,∠AOE=∠1+∠3,
又由题意可知旋转前∠2与∠3重合,∴∠2=∠3,∴∠QND═∠AOE,
∵AB∥CD,∴∠MQN=∠QND,∴∠MQN=∠AOE.
(4)如图3﹣2中,连接BD,在DC上取一点J,使得DJ=AD=![]() ,则AJ=2,
,则AJ=2,
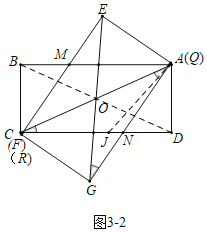
∵CD=2+![]() ,∴CJ=AJ=2,∴∠JCA=∠JAC,
,∴CJ=AJ=2,∴∠JCA=∠JAC,
∵∠AJD=45°=∠JCA+∠JAC,∴∠ACJ=22.5°,
∵OC=OD,∴∠OCD=∠ODC=22.5°,∴∠BOC=45°,
观察图象可知,当点F与点C重合或点G与点D重合时,四边形QMRN的面积最大,最大值=![]() ,
,
∴∠AOE=45°或135°时,四边形QMRN面积最大为![]() .
.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
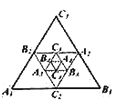
【题目】如图,小红作出了边长为1的第1个等边![]() ,算出了等边
,算出了等边![]() 的面积,然后分别取
的面积,然后分别取![]() 三边的中点
三边的中点![]() 、
、![]() 、
、![]() ,作出了第2个等边
,作出了第2个等边![]() ,算出了等边
,算出了等边![]() 的面积,用同样的方法,作出了第3个等边
的面积,用同样的方法,作出了第3个等边![]() ,算出了等边
,算出了等边![]() 的面积……,由此可得,第
的面积……,由此可得,第![]() 个等边
个等边![]() 的面积是( )
的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小明喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小明从中随机抽取一张卡片是足球社团B的概率是 .
(2)小明先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团D的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
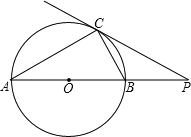
【题目】如图,点P在⊙O外,PC是⊙O的切线,C为切点,直线PO与⊙O相交于点A、B.
(1)若∠A=30°,求证:PA=3PB;
(2)小明发现,∠A在一定范围内变化时,始终有∠BCP=![]() (90°﹣∠P)成立.请你写出推理过程.
(90°﹣∠P)成立.请你写出推理过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
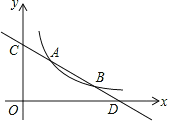
【题目】直线y=kx+b与反比例函数y=![]() (x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
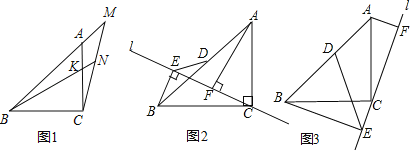
【题目】△ABC是等腰直角三角形,AC=BC,∠ACB=90°
(1)如图1,点M是BA延长线上一点,连结CM,K是AC上一点,BK延长线交CM于N,∠MBN=∠MCA=15°,BK=8,求CM的长度;
(2)如图2,直线l经过点C,AF⊥l于点F,BE⊥l于点E,点D是AB的中点,连接ED,求证:AF=BE+![]() DE;
DE;
(3)将图2中的直线l旋转到△ABC的外部,其他条件不变,请求出AF、BE、DE的关系.并写出必要的步骤.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠B=60,∠ACB=75,点D是BC边上一动点,以AD为直径作⊙O,分别交AB、AC于E、F,若弦EF的最小值为1,则AB的长为
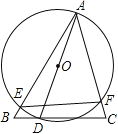
A. | B. | C.1.5 | D. |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=x+3交x轴于点A,交y轴于点B,抛物线y=﹣x2+bx+c经过点A,B.
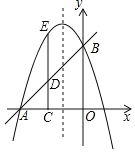
(1)求抛物线解析式;
(2)点C(m,0)在线段OA上(点C不与A,O点重合),CD⊥OA交AB于点D,交抛物线于点E,若DE=![]() AD,求m的值;
AD,求m的值;
(3)点M在抛物线上,点N在抛物线的对称轴上,在(2)的条件下,是否存在以点D,B,M,N为顶点的四边形为平行四边形?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】割圆术是我国古代数学家刘徽创造的一种求周长和面积的方法:随着圆内接正多边形边数的增加,它的周长和面积越来越接近圆周长和圆面积,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽就是大胆地应用了以直代曲、无限趋近的思想方法求出了圆周率.请你也用这个方法求出二次函数![]() 的图象与两坐标轴所围成的图形最接近的面积是( )
的图象与两坐标轴所围成的图形最接近的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com