
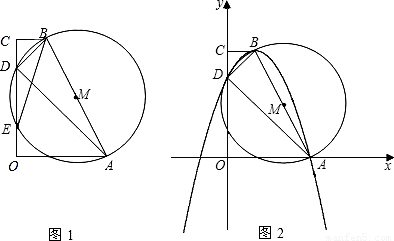
已知:直角梯形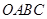 中,
中,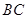 ∥
∥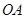 ,∠
,∠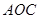 =
=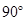 ,以
,以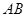 为直径的圆
为直径的圆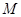 交
交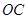 于点
于点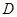 、
、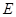 ,连结
,连结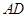 、
、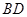 、
、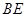 .
.
(1)在不添加其他字母和线的前提下,直接写出图1中的两对相似三角形:
_____________________,______________________ ;
(2)直角梯形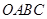 中,以
中,以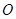 为坐标原点,
为坐标原点,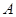 在
在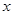 轴正半轴上建立直角坐标系(如图2),若抛物线
轴正半轴上建立直角坐标系(如图2),若抛物线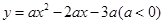 经过点
经过点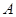 、
、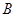 、
、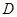 ,且
,且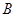 为抛物线的顶点.
为抛物线的顶点.
①写出顶点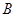 的坐标(用含
的坐标(用含 的代数式表示)___________;
的代数式表示)___________;
②求抛物线的解析式;
③在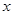 轴下方的抛物线上是否存在这样的点
轴下方的抛物线上是否存在这样的点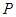 ,过点
,过点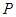 作
作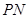 ⊥
⊥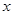 轴于点
轴于点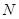 ,使得以点
,使得以点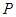 、
、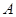 、
、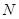 为顶点的三角形与△
为顶点的三角形与△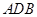 相似?若存在,求出点
相似?若存在,求出点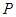 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(1)△ ∽△
∽△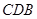 ,△
,△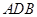 ∽△
∽△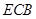 .……………4分
.……………4分
(2)①(1,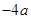 )…………………………………………1分
)…………………………………………1分
②抛物线的解析式为: ………………3分
………………3分
③当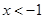 时,点
时,点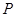 为(
为(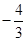 ,
,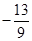 )、(
)、(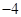 ,
,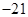 )………………2分
)………………2分
当 时,两个点
时,两个点 不存在 …………………………………2分
不存在 …………………………………2分
【解析】(1)由圆周角定理知:∠ADB=90°,首先可联想到的相似三角形是△BCD和△DOA;易知∠BAD=∠BED,可得的另一对相似三角形是Rt△ABD和Rt△EBC;
(2)①用公式法或配方法均能求出顶点B的坐标;
②根据抛物线的解析式,易求得B、D、A的坐标,也就得到了OA、OD、CD、BC的长,根据(1)得出的相似三角形,即可根据对应的成比例线段求出a的值,也就能求出抛物线的解析式;
③由②易知△OAD是等腰Rt△,若△PAN与△OAD相似,则△PAN也必须是等腰Rt△;可根据抛物线的解析式设出P点坐标,然后根据PN=AN的条件来求出P点的坐标


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2012届浙江省衢州华茂外国语学校九年级上学期期末检测数学试卷(带解析) 题型:解答题
已知:直角梯形 中,
中,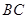 ∥
∥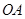 ,∠
,∠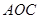 =
=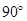 ,以
,以 为直径的圆
为直径的圆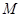 交
交 于点
于点 、
、 ,连结
,连结 、
、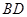 、
、 .
.
(1)在不添加其他字母和线的前提下,直接写出图1中的两对相似三角形:
_____________________,______________________ ;
(2)直角梯形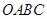 中,以
中,以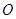 为坐标原点,
为坐标原点, 在
在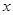 轴正半轴上建立直角坐标系(如图2),若抛物线
轴正半轴上建立直角坐标系(如图2),若抛物线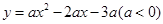 经过点
经过点 、
、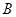 、
、 ,且
,且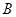 为抛物线的顶点.
为抛物线的顶点.
①写出顶点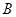 的坐标(用含
的坐标(用含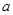 的代数式表示)___________;
的代数式表示)___________;
②求抛物线的解析式;
③在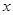 轴下方的抛物线上是否存在这样的点
轴下方的抛物线上是否存在这样的点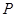 ,过点
,过点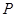 作
作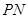 ⊥
⊥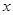 轴于点
轴于点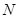 ,使得以点
,使得以点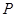 、
、 、
、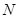 为顶点的三角形与△
为顶点的三角形与△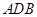 相似?若存在,求出点
相似?若存在,求出点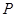 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:2011届云南省昭通市高中(中专)招生统一模拟考试数学试卷(4)(带解析) 题型:解答题
如图所示,已知在直角梯形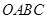 中,
中,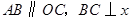 轴于点
轴于点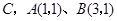 .动点
.动点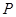 从
从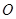 点出发,沿
点出发,沿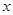 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过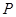 点作
点作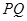 垂直于直线
垂直于直线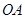 ,垂足为
,垂足为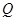 .设
.设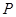 点移动的时间为
点移动的时间为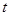 秒(
秒(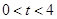 ),
),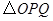 与直角梯形
与直角梯形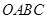 重叠部分的面积为
重叠部分的面积为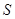 .
.
(1)求经过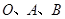 三点的抛物线解析式;
三点的抛物线解析式;
(2)求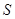 与
与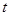 的函数关系式;
的函数关系式;
(3)将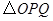 绕着点
绕着点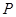 顺时针旋转
顺时针旋转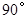 ,是否存在
,是否存在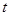 ,使得
,使得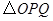 的顶点
的顶点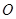 或
或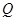 在抛物线上?若存在,直接写出
在抛物线上?若存在,直接写出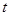 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2010-2011学年江苏省姜堰市初二下学期期中考试数学卷 题型:解答题
如图所示,已知在直角梯形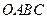 中,
中,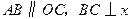 轴于点
轴于点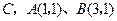 .动点
.动点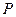 从
从 点出发,沿
点出发,沿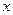 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过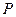 点作
点作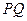 垂直于直线
垂直于直线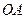 ,垂足为
,垂足为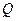 .设
.设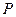 点移动的时间为
点移动的时间为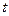 秒(
秒(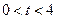 ),
),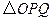 与直角梯形
与直角梯形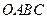 重叠部分的面积为
重叠部分的面积为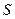 .
.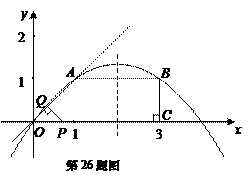
(1)求经过 三点的抛物线解析式;
三点的抛物线解析式;
(2)求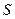 与
与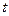 的函数关系式;
的函数关系式;
(3)将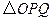 绕着点
绕着点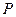 顺时针旋转
顺时针旋转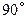 ,是否存在
,是否存在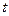 ,使得
,使得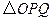 的顶点
的顶点 或
或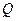 在抛物线上?若存在,直接写出
在抛物线上?若存在,直接写出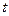 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2010-2011学年云南省昭通市(中专)高中招生统一模拟考试数学试卷(4)(解析版) 题型:解答题
如图所示,已知在直角梯形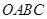 中,
中,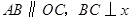 轴于点
轴于点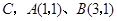 .动点
.动点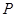 从
从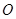 点出发,沿
点出发,沿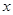 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过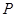 点作
点作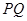 垂直于直线
垂直于直线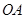 ,垂足为
,垂足为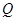 .设
.设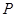 点移动的时间为
点移动的时间为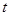 秒(
秒(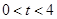 ),
),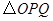 与直角梯形
与直角梯形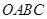 重叠部分的面积为
重叠部分的面积为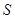 .
.
(1)求经过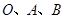 三点的抛物线解析式;
三点的抛物线解析式;
(2)求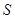 与
与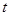 的函数关系式;
的函数关系式;
(3)将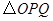 绕着点
绕着点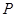 顺时针旋转
顺时针旋转 ,是否存在
,是否存在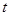 ,使得
,使得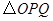 的顶点
的顶点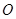 或
或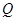 在抛物线上?若存在,直接写出
在抛物线上?若存在,直接写出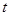 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年山东省济南市九年级下学期模拟考试数学卷(解析版) 题型:解答题
如图所示,已知在直角梯形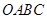 中,
中,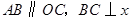 轴于点
轴于点 .动点
.动点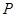 从
从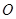 点出发,沿
点出发,沿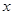 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过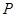 点作
点作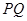 垂直于直线
垂直于直线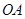 ,垂足为
,垂足为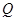 .设
.设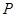 点移动的时间为
点移动的时间为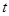 秒(
秒(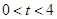 ),
),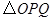 与直角梯形
与直角梯形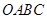 重叠部分的面积为
重叠部分的面积为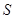 .
.

(1)求经过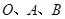 三点的抛物线解析式;
三点的抛物线解析式;
(2)将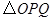 绕着点
绕着点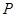 顺时针旋转
顺时针旋转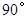 ,是否存在
,是否存在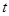 ,使得
,使得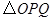 的顶点
的顶点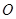 或
或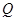 在抛物线上?若存在,直接写出
在抛物线上?若存在,直接写出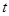 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)求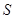 与
与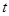 的函数关系式.
的函数关系式.
【解析】(1)设抛物线解析式为y=ax2+bx,把已知坐标代入求出抛物线的解析式(2)根据旋转的性质,代入解析式,判断是否存在(3)求出S的面积,根据t的取值不同分三种情况讨论S与t的函数关系式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com