
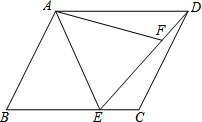
 如图,在?ABCD中,E为BC边上的一点,将△ABE沿AE翻折得到△AFE,点F恰好落在线段DE上.
如图,在?ABCD中,E为BC边上的一点,将△ABE沿AE翻折得到△AFE,点F恰好落在线段DE上.分析 (1)由平行四边形的性质和翻折的性质得出∠B=∠ADC,∠B=∠AFE,得出∠AFE=∠ADC,即可得出结论;
(2)过点D作DG⊥BE,交BE的延长线于点G.由平行四边形的性质得出∠2=∠B,∠3=∠EAD,由翻折的性质得出∠B=∠AFE,∠3=∠4,得出∠4=∠EAD.得出ED=AD=6,由三角函数得出DG=2CG,根据勾股定理得出DG2+CG2=CD2,求出CG、DG,再根据勾股定理求出EG,即可得出EC.
解答 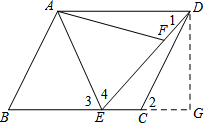 (1)证明:∵四边形ABCD是平行四边形,
(1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠ADC,
∵将△BAE沿AE翻折得到△FAE,点F恰好落在线段DE上,
∴△ABE≌△AFE,
∴∠B=∠AFE,
∴∠AFE=∠ADC,
∵∠FAD=∠AFE-∠1,∠CDE=∠ADC-∠1,
∴∠FAD=∠CDE;
(2)过点D作DG⊥BE,交BE的延长线于点G.
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,CD=AB=5,
∴∠2=∠B,∠3=∠EAD,
由(1)可知,△ABE≌△AFE,
∴∠B=∠AFE,∠3=∠4,
∴∠4=∠EAD,
∴ED=AD=6,
在Rt△CDG中,tan∠2=tan∠ABC=$\frac{DG}{CG}$=2,
∴DG=2CG,
∵DG2+CG2=CD2,
∴(2CG)2+CG2=52,
∴CG=$\sqrt{5}$,DG=2$\sqrt{5}$,
在Rt△EDG中,
∵EG2+DG2=DE2,
∴EG=4,
∴EC=4-$\sqrt{5}$.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质、翻折变换、勾股定理;熟练掌握平行四边形和翻折变换的性质,并能进行推理计算是解决问题的关键.


科目:初中数学 来源: 题型:选择题
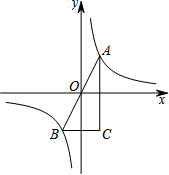 如图,A,B是函数y=$\frac{2}{x}$的图象上关于原点对称的任意两点,BC∥x轴,AC∥y轴,如果△ABC的面积记为S,那么( )
如图,A,B是函数y=$\frac{2}{x}$的图象上关于原点对称的任意两点,BC∥x轴,AC∥y轴,如果△ABC的面积记为S,那么( )| A. | S=4 | B. | S=2 | C. | 2<S<4 | D. | S>4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对载人航天器“嫦娥二号”零部件的检查,采用抽样调查的方式 | |
| B. | 了解炮弹的杀伤力,采用全面调查的方式 | |
| C. | 对电视剧《来自星星的你》收视率的调查,采用全面调查的方式 | |
| D. | 对建阳市食品合格情况的调查,采用抽样调查的方式 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
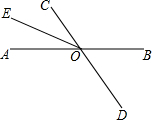 如图,直线AB、CD相交于点O,射线OE平分∠AOC,若∠BOD=68°,则∠BOE等于( )
如图,直线AB、CD相交于点O,射线OE平分∠AOC,若∠BOD=68°,则∠BOE等于( )| A. | 34° | B. | 112° | C. | 146° | D. | 148° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com