
某公司营销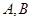 两种产品,根据市场调研,发现如下信息:
两种产品,根据市场调研,发现如下信息:
信息1:销售 种产品所获利润
种产品所获利润 (万元)与所售产品
(万元)与所售产品 (吨)之间存在二次函数关系
(吨)之间存在二次函数关系 .当
.当 时,
时, ;当
;当 时,
时, .
.
信息2:销售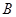 种产品所获利润
种产品所获利润 (万元)与所售产品
(万元)与所售产品 (吨)之间存在正比例函数关系
(吨)之间存在正比例函数关系 .
.
根据以上信息,解答下列问题:(1)求二次函数解析式;
(2)该公司准备购进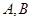 两种产品共10吨,请设计一个营销方案,使销售
两种产品共10吨,请设计一个营销方案,使销售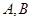 两种产品获得的利润之和最大,最大利润是多少?
两种产品获得的利润之和最大,最大利润是多少?
见解析
解析试题分析:(1)因为当x=1时,y=1.4;当x=3时,y=3.6,代入
得 解得
解得 ,所以,二次函数解析式为y=-0.1x2+1.5x;
,所以,二次函数解析式为y=-0.1x2+1.5x;
(2)设购进A产品m吨,购进B产品(10-m)吨,销售A、B两种产品获得的利润之和为W元,根据题意可列函数关系式为:W=-0.1m2+1.5m+0.3(10-m)=-0.1m2+1.2m+3=-0.1(m-6)2+6.6,因为-0.1<0,根据二次函数的性质知当m=6时,W有最大值6.6,
试题解析:(1)∵当x=1时,y=1.4;当x=3时,y=3.6,
∴
解得 ,
,
所以,二次函数解析式为y=-0.1x2+1.5x; 3分
(2)设购进A产品m吨,购进B产品(10-m)吨,销售A、B两种产品获得的利润之和为W元,
则W=-0.1m2+1.5m+0.3(10-m)=-0.1m2+1.2m+3=-0.1(m-6)2+6.6,
∵-0.1<0,
∴当m=6时,W有最大值6.6,
∴购进A产品6吨,购进B产品4吨,销售A、B两种产品获得的利润之和最大,最大利润是6.6万元.
考点:1.待定系数法求解析式.2.二次函数性质.


科目:初中数学 来源: 题型:解答题
小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?
(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,若这种商品每件的销售价每提高0.5元,其销售量就减少10件.问(1)每件售价定为多少元时,才能使利润为640元?(2)每件售价定为多少元时,才能使利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某商场销售一种进价为20元/台的台灯,经调查发现,该台灯每天的销售量W(台),销售单价x(元)满足W=-2x+80,设销售这种台灯每天的利润为y(元).求y与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的表达式.
(2)足球第一次落地点C距守门员多少米?(取 )
)
(3)运动员乙要抢到第二个落点D,他应再向前跑多少米?(取 )
)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线C1的顶点为P(1,0),且过点(0, ).将抛物线C1向下平移h个单位(h>0)得到抛物线C2.一条平行于x轴的直线与两条抛物线交于A、B、C、D四点(如图),且点A、C关于y轴对称,直线AB与x轴的距离是m2(m>0).
).将抛物线C1向下平移h个单位(h>0)得到抛物线C2.一条平行于x轴的直线与两条抛物线交于A、B、C、D四点(如图),且点A、C关于y轴对称,直线AB与x轴的距离是m2(m>0).
(1)求抛物线C1的解析式的一般形式;
(2)当m=2时,求h的值;
(3)若抛物线C1的对称轴与直线AB交于点E,与抛物线C2交于点F.求证:tan∠EDF﹣tan∠ECP=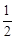 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某公司销售一种进价为20元/个的计算机,其销售量y(万个)与销售价格x(元/个)的变化如下表:
| 价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
| 销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com