
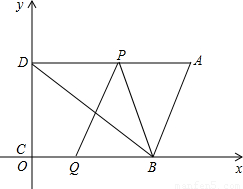
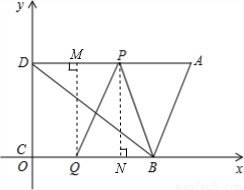
 解:(1)S=
解:(1)S= ×12×t=6t,(0<t≤16);
×12×t=6t,(0<t≤16);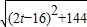 ,BQ=t,PQ=
,BQ=t,PQ=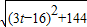 ,
,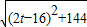 =t,此时方程无实数根;
=t,此时方程无实数根; =
=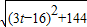 ,
,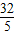 ,t2=0,
,t2=0,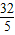 ;
;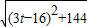 =t,此时方程无实数根;
=t,此时方程无实数根;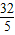 秒时,以B,P,Q三点为顶点的三角形是等腰三角形;
秒时,以B,P,Q三点为顶点的三角形是等腰三角形; =1个单位/秒,
=1个单位/秒, =2个单位/秒,
=2个单位/秒,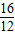 =
= ,
, ,
,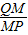 =
=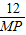 ,
, =
=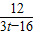 ,
,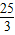 ,
,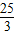 秒时,PQ⊥BD.
秒时,PQ⊥BD.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
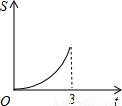
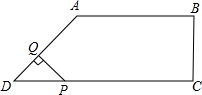 在直角梯形ABCD中,AB∥CD,BC⊥DC于点C,AB=2,CD=3,∠D=45°,动点P从D点出发,沿DC以每秒1个单位长度的速度移动,到C点停止.过P点作PQ垂直于直 线 AD,垂足为Q.设P点移动的时间为t秒,△DPQ与直角梯形ABCD重叠部分的面积为S,下列图象中,能表示S与t的函数关系的图象大致是( )
在直角梯形ABCD中,AB∥CD,BC⊥DC于点C,AB=2,CD=3,∠D=45°,动点P从D点出发,沿DC以每秒1个单位长度的速度移动,到C点停止.过P点作PQ垂直于直 线 AD,垂足为Q.设P点移动的时间为t秒,△DPQ与直角梯形ABCD重叠部分的面积为S,下列图象中,能表示S与t的函数关系的图象大致是( )A、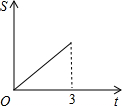 | B、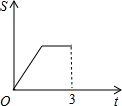 | C、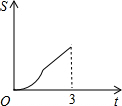 | D、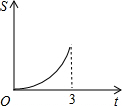 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:单选题
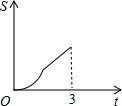
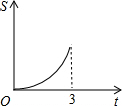
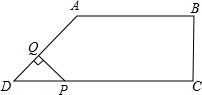 在直角梯形ABCD中,AB∥CD,BC⊥DC于点C,AB=2,CD=3,∠D=45°,动点P从D点出发,沿DC以每秒1个单位长度的速度移动,到C点停止.过P点作PQ垂直于直 线 AD,垂足为Q.设P点移动的时间为t秒,△DPQ与直角梯形ABCD重叠部分的面积为S,下列图象中,能表示S与t的函数关系的图象大致是
在直角梯形ABCD中,AB∥CD,BC⊥DC于点C,AB=2,CD=3,∠D=45°,动点P从D点出发,沿DC以每秒1个单位长度的速度移动,到C点停止.过P点作PQ垂直于直 线 AD,垂足为Q.设P点移动的时间为t秒,△DPQ与直角梯形ABCD重叠部分的面积为S,下列图象中,能表示S与t的函数关系的图象大致是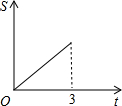
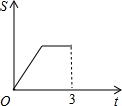
查看答案和解析>>
科目:初中数学 来源:2010年北京市怀柔区中考数学一模试卷(解析版) 题型:选择题

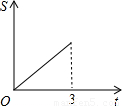
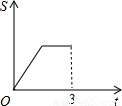

查看答案和解析>>
科目:初中数学 来源: 题型:
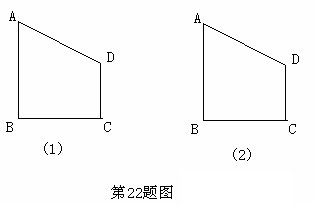
已知直角梯形ABCD中,![]() ,CD//AB,AB=5,CD=3,BC=4。
,CD//AB,AB=5,CD=3,BC=4。
(1)请在图(1)中建立适当的平![]() 面直角坐标系,使B、C的坐标分别为(-2,0)
面直角坐标系,使B、C的坐标分别为(-2,0)
和(0,2),写出点A、D的坐标,并指出它们所在的![]() 象限。
象限。
(2)若要使B、C两点的坐标分别为(-4,-3)和![]() (0,-3
(0,-3![]() ),又应如何建立平面直
),又应如何建立平面直
角坐标呢?请在图(2)中画出你建立的平面直角坐标系,并写出A、D的坐标。
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com