Question

5．在平面直角坐标系xOy中，四边形OABC为矩形，OA在x轴上，OC在y轴正半轴上，且A（10，0），B（0，8）
（1）如图1，在矩形OABC的边上取一点E，连接OE，将△AOE沿OE折叠，使点A恰好落在BC边上的F处，求AE的长．
（2）将矩形OABC的AB边沿x轴负方向平移至MN（其它边保持不动），M，N分别在边OA，CB上且满足CN=OM=OC=MN．
①如图2，P，Q分别是OM，MN上一点，若∠PCQ=45°，求证：PQ=OP+NQ
②如图3，S，G，R，H分别是OC，OM，MN，NC上一点，SR，HG交于点D，若∠SDG=135°，HG=2$\sqrt{20}$，求RS的长．
（3）如图4，在（1）的条件下，擦去折痕OE，EF，连接AF，动点P在线段OF上（动点P与O，F不重合），动点Q在线段OA的延长线上且AQ=FP，连接PQ交AF于点N，作PM⊥AF于M，试问当P、Q在移动过程中线段MN的长度是否发生变化？若不变，求出线段MN的长度，若变化，请说明理由．

Answer 1

分析 （1）设AE=x，在Rt△BEF中，根据勾股定理列方程解出即可；
（2）①作辅助线，构建两个三角形全等，证明△COE≌△CNQ和△ECP≌△QCP，由PE=PQ=OE+OP，得出结论；
②作辅助线，构建平行四边形和全等三角形，可得?CSRE和?CFGH，则CE=SR，CF=GH，证明△CEN≌△CE′O和△E′CF≌△ECF，得EF=E′F，设EN=x，在Rt△MEF中，根据勾股定理列方程求出EN的长，再利用勾股定理求CE，则SR与CE相等，所以SR=$\frac{8\sqrt{10}}{3}$；
（3）在（1）的条件下，当P、Q在移动过程中线段MN的长度不会发生变化，求出MN的长即可；如图4，过P作PD∥OQ，证明△PDF是等腰三角形，由三线合一得：DM=$\frac{1}{2}$FD，证明△PND≌△QNA，得DN=$\frac{1}{2}$AD，则MN=$\frac{1}{2}$AF，由（1）的条件求AF的长，则MN=$\frac{1}{2}$AF=2$\sqrt{5}$．

解答 解：（1）如图1，由题意得：OA=10，AB=8，
设AE=x，则BE=8-x，EF=x，
在Rt△COF中，OC=8，
∵OF=OA=10，
∴CF=6，
∴BF=10-6=4，
由勾股定理得：4²+（8-x）²=x²，
x=5，
∴AE=5；
（2）①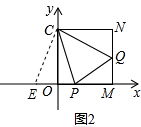如图2，在PO的延长线上取一点E，使NQ=OE，
∵CN=OM=OC=MN，∠COM=90°，
∴四边形OMNC是正方形，
∴CO=CN，
∵∠EOC=∠N=90°，
∴△COE≌△CNQ，
∴CQ=CE，∠ECO=∠QCN，
∵∠PCQ=45°，
∴∠QCN+∠OCP=90°-45°=45°，
∴∠ECP=∠ECO+∠OCP=45°，
∴∠ECP=∠PCQ，
∵CP=CP，
∴△ECP≌△QCP，
∴EP=PQ，
∵EP=EO+OP=NQ+OP，
∴PQ=OP+NQ；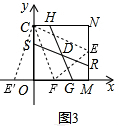
②如图3，过C作CE∥SR，在x轴负半轴上取一点E′，使OE′=EN，得?CSRE，
且△CEN≌△CE′O，则CE=SR，
过C作CF∥GH交OM于F，连接FE，得?CFGH，则CF=GH=2$\sqrt{20}$，
∵∠SDG=135°，
∴∠SDH=180°-135°=45°，
∴∠FCE=∠SDH=45°，
∴∠NCE+∠OCF=45°，
∵△CEN≌△CE′O，
∴∠E′CO=∠ECN，CE=CE′，
∴∠E′CF=∠E′CO+∠OCF=45°，
∴∠E′CF=∠FCE，
∵CF=CF，
∴△E′CF≌△ECF，
∴E′F=EF
在Rt△COF中，OC=8，FC=2$\sqrt{20}$，
由勾股定理得：OF=$\sqrt{（2\sqrt{20}）^{2}-{8}^{2}}$=4，
∴FM=8-4=4，
设EN=x，则EM=8-x，FE=E′F=x+4，
则（x+4）²=4²+（8-x）²，
解得：x=$\frac{8}{3}$，
∴EN=$\frac{8}{3}$，
由勾股定理得：CE=$\sqrt{C{N}^{2}+E{N}^{2}}$，
=$\sqrt{{8}^{2}+（\frac{8}{3}）^{2}}$，
=$\frac{8\sqrt{10}}{3}$，
∴SR=CE=$\frac{8\sqrt{10}}{3}$；
（3）在（1）的条件下，当P、Q在移动过程中线段MN的长度不会发生变化，
如图4，过P作PD∥OQ，交AF于D，
∵OF=OA，
∴∠OFA=∠OAF=∠PDF，
∴PF=PD，
∵PF=AQ，
∴PD=AQ，
∵PM⊥AF，
∴DM=$\frac{1}{2}$FD，
∵PD∥OQ，
∴∠DPN=∠PQA，
∵∠PND=∠QNA，
∴△PND≌△QNA，
∴DN=AN，
∴DN=$\frac{1}{2}$AD，
∴MN=DM+DN=$\frac{1}{2}$DF+$\frac{1}{2}$AD=$\frac{1}{2}$AF，
由（1）知：BF=4，AB=8，
∴AF=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$，
∴MN=2$\sqrt{5}$，
∴在（1）的条件下，当P、Q在移动过程中线段MN的长度不会发生变化，它的长度为2$\sqrt{5}$．

点评 本题是四边形与动点问题的综合题，考查了矩形、正方形、全等三角形等图形的性质与判定；知识点较多，综合性强，注意将矩形OABC的AB边沿x轴负方向平移至MN，得到正方形OMNC时，边长为8；第（2）问中的两个问题思路一致：在正方形外构建与△CNQ全等的三角形，可截取OE=NQ，也可以将△CNQ绕点C顺时针旋转90°得到，再证明另一对三角形全等，得出结论，是常考题型．