
”¾ĢāÄæ”æŌŚRt”÷ABCÖŠ£¬ĪŅĆĒ¹ę¶Ø£ŗŅ»øöČń½ĒµÄ¶Ō±ßÓėŠ±±ßµÄ±ČÖµ³ĘĪŖÕāøöČń½ĒµÄÕżĻŅÖµ£®
ĄżČē£ŗRt”÷ABCÖŠ£¬”ĻC£½90”ć£¬”ĻAµÄ¶Ō±ßBCÓėŠ±±ßABµÄ±ČÖµ£¬¼“![]() ¾ĶŹĒ”ĻAµÄÕżĻŅÖµ£®ĄūÓĆĮæ½ĒĘ÷æÉŅŌÖĘ×÷”°Čń½ĒÕżĻŅÖµĖŁ²éæØ”±£®ÖĘ×÷·½·ØČēĻĀ£ŗ
¾ĶŹĒ”ĻAµÄÕżĻŅÖµ£®ĄūÓĆĮæ½ĒĘ÷æÉŅŌÖĘ×÷”°Čń½ĒÕżĻŅÖµĖŁ²éæØ”±£®ÖĘ×÷·½·ØČēĻĀ£ŗ
ČēĶ¼£¬ÉčOA£½1£¬ŅŌOĪŖŌ²ŠÄ£¬·Ö±šŅŌ0.05£¬0.1£¬0.15£¬0.2£¬”£¬0.9£¬0.95³¤ĪŖ°ė¾¶×÷°ėŌ²£¬ŌŁŅŌOAĪŖÖ±¾¶×÷”ŃM£®ĄūÓĆ”°Čń½ĒÕżĻŅÖµĖŁ²éæØ”±æÉŅŌ¶Į³öĻąÓ¦Čń½ĒÕżĻŅµÄ½üĖĘÖµ£®ĄżČē£ŗ60”ćµÄÕżĻŅÖµŌ¼ŌŚ0.85”«0.88Ö®¼äȔֵ£¬45”ćµÄÕżĻŅÖµŌ¼ŌŚ0.70”«0.72Ö®¼äȔֵ£®ĻĀĮŠ½Ē¶ČÖŠÕżĻŅÖµ×ī½Ó½ü0.94µÄŹĒ£Ø””””£©
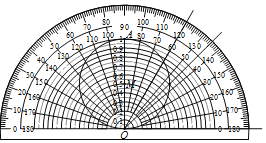
A.30”ćB.50”ćC.40”ćD.70”ć

| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬µć
£¬µć![]() ·Ö±šŹĒ
·Ö±šŹĒ![]() ÉĻµÄµć£¬½«
ÉĻµÄµć£¬½«![]() ŃŲ
ŃŲ![]() ÕŪµž£¬Ź¹µĆµć
ÕŪµž£¬Ź¹µĆµć![]() ĀäŌŚ
ĀäŌŚ![]() ÉĻµÄ
ÉĻµÄ![]() “¦.
“¦.
£Ø1£©Éč![]() µÄ³¤æÉÓĆŗ¬
µÄ³¤æÉÓĆŗ¬![]() µÄ“śŹżŹ½±ķŹ¾ĪŖ________£»
µÄ“śŹżŹ½±ķŹ¾ĪŖ________£»
£Ø2£©Čōµć![]() ŹĒ
ŹĒ![]() µÄÖŠµć£¬Ēó
µÄÖŠµć£¬Ēó![]() µÄ³¤£»
µÄ³¤£»
£Ø3£©Čō![]() £¬ÅŠ¶ĻĖıߊĪ
£¬ÅŠ¶ĻĖıߊĪ![]() µÄŠĪד£¬²¢ĖµĆ÷ĄķÓÉ.
µÄŠĪד£¬²¢ĖµĆ÷ĄķÓÉ.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
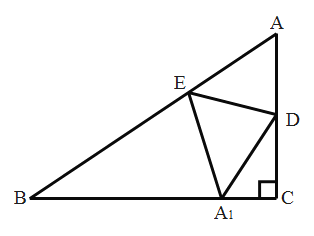
”¾ĢāÄæ”æČēĶ¼£¬¾ŲŠĪABCDÖŠ£¬AB£½m£¬AD£½n£®
£Ø1£©Čōm£½4£¬¾ŲŠĪABCDµÄ±ßCDÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹µĆ”ĻAPB£½90”ć£æŠ“³öµćP“ęŌŚ»ņ²»“ęŌŚµÄæÉÄÜĒéæöŗĶ“ĖŹ±nĀś×ćµÄĢõ¼ž£®
£Ø2£©¾ŲŠĪABCDµÄ±ßÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹µĆ”ĻAPB£½60”ć£æŠ“³öµćP“ęŌŚ»ņ²»“ęŌŚµÄæÉÄÜĒéæöŗĶ“ĖŹ±m”¢nĀś×ćµÄĢõ¼ž£®


²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
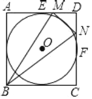
”¾ĢāÄæ”æČēĶ¼£¬”ŃOÄŚĒŠÓŚÕż·½ŠĪABCD£¬±ßAD”¢CD·Ö±šÓė”ŃOĒŠÓŚµćE”¢F£¬µćM”¢N·Ö±šŌŚĻ߶ĪDE”¢DFÉĻ£¬ĒŅMNÓė”ŃOĻąĒŠ£¬Čō”÷MBNµÄĆ껿ĪŖ8£¬Ōņ”ŃOµÄ°ė¾¶ĪŖ£Ø””””£©
A.![]() B.2
B.2![]() C.
C.![]() D.2
D.2![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßy£½ax2+bx©3½»xÖįÓŚµćA£Ø©1£¬0£©ŗĶµćB£Ø3£¬0£©£¬ÓėyÖį½»ÓŚµćC£¬¶„µćŹĒD£¬¶Ō³ĘÖį½»xÖįÓŚµćE£®
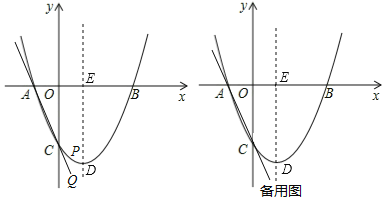
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©µćPŹĒÅ×ĪļĻßŌŚµŚĖÄĻóĻŽÄŚµÄŅ»µć£¬¹żµćP×÷PQ”ĪyÖį£¬½»Ö±ĻßACÓŚµćQ£¬ÉčµćPµÄŗį×ų±źŹĒm£®
¢ŁĒóĻ߶ĪPQµÄ³¤¶Čn¹ŲÓŚmµÄŗÆŹż¹ŲĻµŹ½£»
¢ŚĮ¬½ÓAP£¬CP£¬Ēóµ±”÷ACPĆ껿ĪŖ![]() Ź±µćPµÄ×ų±ź£»
Ź±µćPµÄ×ų±ź£»
£Ø3£©ČōµćNŹĒÅ×ĪļĻ߶Ō³ĘÖįÉĻŅ»µć£¬ŌņÅ×ĪļĻßÉĻŹĒ·ń“ęŌŚµćM£¬Ź¹µĆŅŌµćB£¬C£¬M£¬NĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öĻ߶ĪBNµÄ³¤¶Č£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĮŠ·½³Ģ»ņ·½³Ģ×é½āÓ¦ÓĆĢā£ŗ
”°ĆĄ»Æ³ĒŹŠ£¬øÄÉĘČĖĆń¾Ó×”»·¾³”±ŹĒ³ĒŹŠ½ØÉčµÄŅ»ĻīÖŲŅŖÄŚČŻ£®Ä³ŹŠ½üÄźĄ“£¬ĶعżÖ²²Ż”¢ŌŌŹ÷”¢ŠŽ½Ø¹«Ō°µČ“ėŹ©£¬Ź¹³ĒĒųĀĢµŲĆ껿²»¶ĻŌö¼Ó£¬2011Äźµ×øĆŹŠ³ĒĒųĀĢµŲ×ÜĆ껿Ō¼ĪŖ75¹«Ēź£¬½ŲÖ¹µ½2013Äźµ×£¬øĆŹŠ³ĒĒųĀĢµŲ×ÜĆ껿Ō¼ĪŖ108¹«Ēź£¬Ēó“Ó2011Äźµ×ÖĮ2013Äźµ×øĆŹŠ³ĒĒųĀĢµŲ×ÜĆ껿µÄÄźĘ½¾łŌö³¤ĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÅ×ĪļĻßy=x2©2x©3Óė½»yÖįøŗ°ėÖįÓŚCµć£¬Ö±Ļßy=kx+2½»Å×ĪļĻßÓŚE”¢FĮ½µć£ØEµćŌŚFµć×ó±ß£©£®Ź¹”÷CEF±»yÖį·Ö³ÉµÄĮ½²æ·ÖĆ껿²īĪŖ5£¬ŌņkµÄÖµĪŖ_____£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ¼×”¢ŅŅĮ½øö²»ĶøĆ÷µÄŗŠ×ÓÖŠ£¬·Ö±š×°ÓŠ³żŃÕÉ«ĶāĘäĖüĶźČ«ĻąĶ¬µÄŠ”Ēņ£¬ĘäÖŠ£¬¼×ŗŠ×Ó×°ÓŠ2øö°×Ēņ£¬1øöŗģĒņ£»ŅŅŗŠ×Ó×°ÓŠ2øöŗģĒņ£¬1øö°×Ēņ£®
£Ø1£©½«¼×ŗŠ×ÓŅ”ŌČŗó£¬Ė껜Ȕ³öŅ»øöŠ”Ēņ£¬ĒóŠ”ĒņŹĒ°×É«µÄøÅĀŹ£»
£Ø2£©Š”»ŖŗĶĶ¬×ĄÉĢ¶Ø£ŗ½«Į½øöŗŠ×ÓŅ”ŌČŗó£¬ø÷Ė껜ƞ³öŅ»øöŠ”Ēņ£®ČōŃÕÉ«ĻąĶ¬£¬ŌņŠ”»Ŗ»ńŹ¤£»ČōŃÕÉ«²»Ķ¬£¬ŌņĶ¬×Ą»ńŹ¤£¬ĒėÓĆĮŠ±ķ·Ø»ņ»³öŹ÷דĶ¼µÄ·½·ØĖµĆ÷ĖÓ®µÄæÉÄÜŠŌ“ó£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ“ü֊װӊ2øöŗģĒņŗĶ2øöĀĢĒņ£®
£Ø1£©ĻČ“Ó“üÖŠĆž³ö1øöĒņŗó·Å»Ų£¬»ģŗĻ¾łŌČŗóŌŁĆž³ö1øöĒņ£¬ĒóĮ½“ĪĆžµ½µÄĒņÖŠÓŠ1øöĀĢĒņŗĶ1øöŗģĒņµÄøÅĀŹ£»
£Ø2£©ĻČ“Ó“üÖŠĆž³ö1øöĒņŗó²»·Å»Ų£¬ŌŁĆž³öøöĒņ£¬ŌņĮ½“ĪĆžµ½µÄĒņÖŠÓŠ1øöĀĢĒņŗĶ1øöŗģĒņµÄøÅĀŹŹĒ”” ””£®£ØÖ±½ÓĢī“š°ø£©
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com