
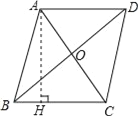
【题目】如图,在ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8.
(1)求证:四边形ABCD是菱形;
(2)过点A作AH⊥BC于点H,求AH的长.

【答案】(1)证明见解析;(2)![]()
【解析】试题(1)由平行四边形的对角线互相平分得到△AOB的两条边OA、OB的长度,则根据勾股定理的逆定理判定∠AOB=90°,即平行四边形的对角线互相垂直平分,故四边形ABCD是菱形.
(2)根据菱形的不变性,用不同方法求面积:平行四边形的面积=菱形的面积,可求解.
试题解析:(1)证明:∵在![]() ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8,
ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8,
∴AO=![]() AC=3,BO=
AC=3,BO=![]() BD=4,
BD=4,
∵AB=5,且32+42=52,
∴AO2+BO2=AB2,
∴△AOB是直角三角形,且∠AOB=90°,
∴AC⊥BD,
∴四边形ABCD是菱形;
(2)解:如图所示:
∵四边形ABCD是菱形,
∴BC=AB=5,
∵S△ABC=![]() ACBO=
ACBO=![]() BCAH,
BCAH,
∴![]() ×6×4=
×6×4=![]() ×5×AH,
×5×AH,
解得:AH=![]() .
.


科目:初中数学 来源: 题型:
【题目】请你用学习“一次函数”时积累的经验和方法解决下列问题:
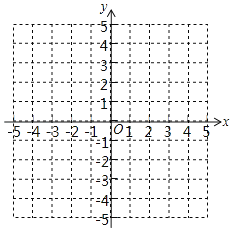
(1)在平面直角坐标系中,画出函数y=|x|的图象:
①列表填空:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
|
|
| … |
②描点、连线,画出y=|x|的图象;
(2)结合所画函数图象,写出y=|x|两条不同类型的性质;
(3)结合所画函数图象,求方程|x|﹣2x﹣1=0的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右依次记为A1、A2、A3、…、An,已知第1个正方形中的一个顶点A1的坐标为(1,1),则点A2015的纵坐标为( )

A.2015B.2014C.22014D.22015
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,点A的坐标为![]() ,点B坐标为
,点B坐标为![]() 满足
满足![]() .
.
(1)若![]() 没有平方根,判断点A在第几象限并说明理由;
没有平方根,判断点A在第几象限并说明理由;
(2)若点A到![]() 轴的距离是点B到
轴的距离是点B到![]() 轴距离的3倍,求点B的坐标;
轴距离的3倍,求点B的坐标;
(3)点D的坐标为(4,-2),△OAB的面积是△DAB面积的2倍,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90o,AB=AD,AE=AC, AF⊥CF,垂足为F.
(1)若AC=10,求四边形ABCD的面积;
(2)求证:AC平分∠ECF;
(3)求证:CE=2AF .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两块等腰直角三角板△ABC和△DEC如图摆放,其中∠ACB=∠DCE=90°,F是DE的中点,H是AE的中点,G是BD的中点.
(1)如图1,若点D、E分别在AC、BC的延长线上,通过观察和测量,猜想FH和FG的数量关系为______和位置关系为______;
(2)如图2,若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时,其余条件均不变,则(1)中的猜想是否还成立,若成立,请证明,不成立请说明理由;
(3)如图3,将图1中的△DEC绕点C顺时针旋转一个锐角,得到图3,(1)中的猜想还成立吗?直接写出结论,不用证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角板按如图放置,则下列结论:①如果∠2=30°,则有AC∥DE;②如果BC∥AD,则有∠2=45°;③∠BAE+∠CAD随着∠2的变化而变化;④如果∠2=30°,那么∠4=45°;正确的( )

A.①②③
B.①②④
C.①③④
D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com