练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．已知多项式x2+px+q可分解为（x+3）（x-2），则p=1，q=-6．

    分析 因式分解结果利用多项式乘以多项式法则计算，再利用多项式相等的条件求出p与q的值即可．

    解答 解：根据题意得：x2+px+q=（x+3）（x-2）=x2+x-6，
    则p=1，q=-6，
    故答案为：1；-6

    点评 此题考查了因式分解-十字相乘法，多项式乘以多项式，以及多项式相等的条件，熟练掌握十字相乘法是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    12．下列计算正确的是（　　）
    A．（-2）0=-1B．x3•x4=x12C．（-mn）3•（-mn）2=-m3n3D．$\sqrt{\frac{-3}{-5}}$=$\frac{\sqrt{-3}}{\sqrt{-5}}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图，在△ABC中，AB=AC=28cm，BC=20cm，点D是AB边的中点，若有一动点P在BC边上由点B向点C运动，点Q在CA边上由点C向A运动．
    （1）P、Q两点的运动速度均为3cm/s，经过2秒后，△BPD与△CPQ是否全等，说明理由
    （2）若点P的运动速度为2.5cm/s，点Q的运动速度为3.5cm/s，是否存在某一时刻，使△BPD≌△CQP．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．已知二次函数C1：y=-ax2+bx+3a的图象经过点M（1，0）、N（0，-3），其关于原点对称后的二次函数C2与x轴交于A、B两点（点B在点A右侧）与y轴交与点C，其抛物线的顶点为D．
    （1）求对称后的二次函数C2的解析式；
    （2）作出抛物线C2的图象，连接DC、BC、DB，求证：△BCD是直角三角形；
    （3）在抛物线C2图象的对称轴右侧的抛物线上是否存在点P，使得△PDC为等腰三角形？若存在，求出符合条件的点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．用“描点法”画二次函数y=ax2+bx+c的图象时，列了如下表格：
    x…-2-1012…
    y…6.5-4-2.5-2-2.5…
    根据表格中的信息回答问题，该二次函数y=ax2+bx+c在x=3时，函数值y=-4．．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

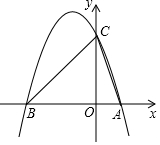    7．如图，在平面直角坐标系中，y=ax2+bx+c（a＜0）与x轴交于点A（x1，0），B（x2，0）两点（x2＜0＜x1），与y轴正半轴交于点C．已知OA：OB=1：3，OB=OC，△ABC的面积S△ABC=6．
    （1）求经过A、B、C三点的抛物线的函数表达式；
    （2）设E是y轴左侧抛物线上异于点B的一个动点，过点E作x轴的平行线交抛物线于另一点F，过点F作FG垂直于x轴于点G，再过点E作EH垂直于x轴于点H，得到矩形EFGH．则在点E的运动过程中，当矩形EFGH为正方形时，求出该正方形的边长；
    （3）在抛物线上是否存在异于B、C的点M，使△MBC中BC边上的高为2$\sqrt{2}$？若存在，求出点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．2015年9月14日，意大利物理学家马尔科•德拉戈收到来自激光干涉引力波天文台（LIGO）的系统自动提示邮件，一股宇宙深处的引力波到达地球，在位于美国华盛顿和烈文斯顿的两个LIGO探测器上产生了4×10-18米的空间畸变（如图中的引力波信号图象所示），也被称作“时空中的涟漪”，人类第一次探测到了引力波的存在，“天空和以前不同了…你也听得到了．”这次引力波的信号显著性极其大，探测结果只有三百五十万分之一的误差．三百五十万分之一约为0.0000002857．将0.0000002857用科学记数法表示应为（　　）
    A．2.857×10-8B．2.857×10-7C．2.857×10-6D．0.2857×10-6

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．地球赤道半径约为6378千米，这个数据用科学记数法表示为（　　）千米．
    A．6.378×104B．63.78×102C．6378×10-4D．6.378×103

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

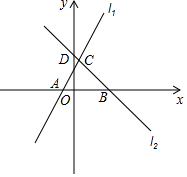    12．如图，直线l1，l2交于点C，直线l1与x轴交于A；直线l2与x轴交于B（3，0），与y轴交于D（0，3），已知直线l1的函数解析式为y=2x+2．
    （1）求直线l2的解析式和交点C的坐标．
    （2）将直线l1向下平移a个单位使之经过B，与y轴交于E．
    ①求△CBE的面积；
    ②若点Q为y轴上一动点，当△EBQ为等腰三角形时，求出Q的坐标．

    查看答案和解析>>

    同步练习册答案