
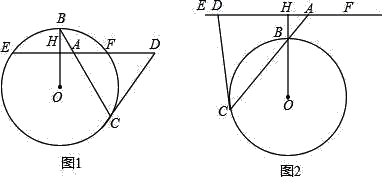
【题目】如图1,A为⊙O的弦EF上的一点,OB是和这条弦垂直的半径,垂足为H,BA的延长线交⊙O于点C,过点C作⊙O的切线与EF的延长线相交于点D.
(1)求证:DA=DC;
(2)当DF:EF=1:8,且DF=![]() 时,求ABAC的值;
时,求ABAC的值;
(3)将图1中的EF所在直线往上平行移动到⊙O外,如图2的位置,使EF与OB,延长线垂直,垂足为H,A为EF上异于H的一点,且AH小于⊙O的半径,AB的延长线交⊙O于C,过C作⊙O的切线交EF于D.试猜想DA=DC是否仍然成立?并证明你的结论.
【答案】(1)见解析;(2)24;(3)见解析.
【解析】
(1)连接过切点的半径OC,根据等角的余角相等进行证明∠ACD=∠DAC,从而得到AD=CD;
(2)根据已知条件求得DF的长,再根据切割线定理求得CD的长.从而求得DF和EF的长,最后根据相交弦定理即可求得它们的乘积;
(3)作直径,构造了直角三角形,也构造了弦切角所夹的弧所对的圆周角.根据等角的余角相等证明∠DAC=∠ACD,从而证明结论.
(1)连接OC,则OC⊥DC,
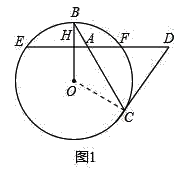
∴∠DCA=90°﹣∠ACO=90°﹣∠B,
∵∠DAC=∠BAE=90°﹣∠B,
∴∠DAC=∠DCA,
∴DA=DC;
(2)∵DF:EF=1:8,
∵DF=![]() ,
,
∴EF=8DF=8![]() ,
,
∵DC为⊙O的切线,
∴DC2=DFDE=![]() ×9
×9![]() =18,
=18,
∵DC=3![]() ,
,
∴AF=2![]() ,AE=6
,AE=6![]() ,
,
∴ABAC=AEAF=24;
(3)结论DA=DC仍然成立.
理由如下:延长BO交⊙O于K,连接CK,则∠KCB=90°,
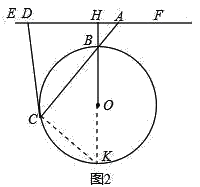
∵DC为⊙O的切线,
∴∠DCA=∠CKB=90°﹣∠CBK,
∵∠CBK=∠HBA,
∴∠BAH=90°﹣∠HBA=90°﹣∠CBK,
∴∠DCA=∠BAH,
∴DA=DC.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=72°.

(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
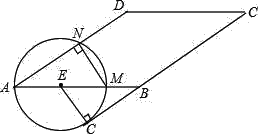
【题目】如图,在ABCD(AB>AD)中,点E在边AB上,以点E为圆心,AE长为半径的⊙E分别交AB、AD于点N、N,与BC所在的直线相切于点G
(1)求证:EG∥MN;
(2)若AB=10,AD与BC之间的距离为6,求⊙E的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且∠B= 60°.过点C作圆的切线l与直径AD的延长线交于点E,AF⊥l,垂足为F,CG⊥AD,垂足为G.
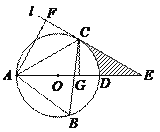
(1)求证:△ACF≌△ACG;
(2)若AF= 4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是等边三角形,
是等边三角形,![]() 是中线,延长
是中线,延长![]() 到点
到点![]() ,使
,使![]() ,连结
,连结![]() ,下面给出的四个结论:①
,下面给出的四个结论:①![]() ,②
,②![]() 平分
平分![]() ,③
,③![]() ,④
,④![]() ,其中正确的个数是( )
,其中正确的个数是( )
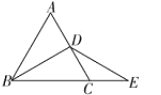
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;如果P、Q两动点同时运动,那么何时△QBP与△ABC相似?
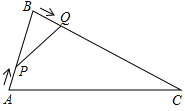
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com