
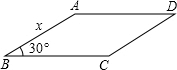
 如图所示,已知平行四边形ABCD的周长为8cm,∠B=30°,若边长AB=x(cm).
如图所示,已知平行四边形ABCD的周长为8cm,∠B=30°,若边长AB=x(cm). 解:(1)过A作AE⊥BC于E,如图,
解:(1)过A作AE⊥BC于E,如图, x,
x, x(4-x)=-
x(4-x)=- x2+2x(0<x<4);
x2+2x(0<x<4); x2+2x
x2+2x (x-2)2+2,
(x-2)2+2, ,
, x,利用平行四边的周长可表示出BC=4-x,则0<x<4;然后根据平行四边形的面积公式即可得到y(cm2)与x的函数关系式;
x,利用平行四边的周长可表示出BC=4-x,则0<x<4;然后根据平行四边形的面积公式即可得到y(cm2)与x的函数关系式; (x-2)2+2,然后根据二次函数的最值问题即可得到x取什么值时,y的值最大,并得到最大值.
(x-2)2+2,然后根据二次函数的最值问题即可得到x取什么值时,y的值最大,并得到最大值.

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
 在八年级上册我们已经知道三角形的中位线具有如下性质:
在八年级上册我们已经知道三角形的中位线具有如下性质:| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 57、如图所示,已知?ABCD,试用两种方法,将?ABCD分成面积相等的四个部分.(要求用文字简述你所设计的两种方法,并在所给的两个平行四边形中正确画图).
57、如图所示,已知?ABCD,试用两种方法,将?ABCD分成面积相等的四个部分.(要求用文字简述你所设计的两种方法,并在所给的两个平行四边形中正确画图).查看答案和解析>>
科目:初中数学 来源: 题型:
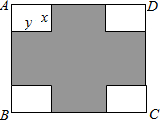 衔接处用总长为72米的矮篱笆隔开.
衔接处用总长为72米的矮篱笆隔开.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com