练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在四边形ABCD中，已知A、B、C、D的坐标分别为（0，2）、（1，0）、（6，2）、（2，4）．
    （1）在坐标系中画出四边形ABCD；
    （2）求四边形ABCD的面积．

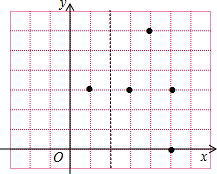
    解：（1）如图所示．
    （2）根据图示知：
    S△ABC+S△ADC=S四边形ABCD，
    ∵S△ABC=AC•BE=×6×2=6，
    S△ADC=AC•DF=×6×1=3；
    ∴S四边形ABCD=6+3=9．
    分析：（1）根据图中的点A、B、C、D的坐标分别为（0，2）、（1，0）、（6，2）、（2，4），顺次连接各个点；
    （2）将四边形ACBD的面积分为两部分：S△ABC和S△ADC，然后根据三角形的面积公式分别求出这两个三角形的面积．
    点评：本题考查了三角形的面积、坐标与图形性质．解答该题的关键是根据点A、B、C、D的坐标求出线段AC、DF、BE的长度．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    11、如图所示，在四边形ABCD中，BD是它的一条对角线，若∠1=∠2，∠A=55°16′，则∠ADC=
    124°44′
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在四边形ABCD中，AD=4cm，CD=3cm，AD⊥CD，AB=13cm，BC=12cm，求四边形的面积．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    6、在四边形ABCD中，AD∥BC，AB=DC，则四边形ABCD是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在四边形ABCD中，∠A，∠B，∠C，∠D的度数之比为2：3：4：3，则∠C的外角等于（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在四边形ABCD中，AD=BC，P是对角线BD的中点，M是边DC的中点，N是边AB的中点．△MPN是什么三角形？为什么？

    查看答案和解析>>

    同步练习册答案