【题目】如图，∠DAB＝∠CAE，AD＝AB，AC＝AE．
（1）求证△ABE≌△ADC；
（2）设BE与CD交于点O，∠DAB＝30°，求∠BOC的度数．
【答案】（1）见解析；（2）150°.
【解析】
（1）先利用角的和差证出∠DAC=∠BAE，再利用SAS证△ABE≌△ADC即可；
（2）设AB与OD交于点F，根据（1）中全等可得：∠ABE=∠D，根据三角形的内角和定理可证∠BOF=∠DAB=30°，从而求出∠BOC的度数.
解：（1）∵∠DAB＝∠CAE
∴∠DAB＋∠BAC＝∠CAE＋∠BAC
∴∠DAC=∠BAE
在△ABE和△ADC中
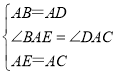
∴△ABE≌△ADC；
（2）设AB与OD交于点F
∵△ABE≌△ADC
∴∠ABE=∠D
∵∠BFO=∠DFA
∴∠BOF=180°－∠ABE－∠BFO=180°－∠D－∠DFA=∠DAB=30°
∴∠BOC=180°－∠BOF=150°
科目：初中数学 来源： 题型：
【题目】 P为等边△ABC的边AB上一点，Q为BC延长线上一点，且PA＝CQ，连PQ交AC边于D．
（1）证明：PD＝DQ．
（2）如图2，过P作PE⊥AC于E，若AB＝6，求DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某省为推广新能源汽车，计划连续五年给予财政补贴．补贴开始时间为
年度，截止时间为
年度．补贴期间后一年度的补贴额均在前一年度补贴额基础上递增．计划前三年，每年度按固定额度
亿元递增；后两年均在上一年的基础上按相同增长率递增．已知
年度计划补贴额为
亿元．
若
年度计划补贴额比年度至少增加
，求的取值范围；
若预计
这五年补贴总额比年度补贴额的
倍还多
亿元，求后两年财政补贴的增长率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点．
（1）在图1中以格点为顶点画一个面积为10的正方形；
（2）在图2中以格点为顶点画一个三角形，使三角形三边长分别为2、
、
；
（3）如图3，点A、B、C是小正方形的顶点，求∠ABC的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=CD=4 cm，则球的半径长是（ ）
A. 2cm B. 2.5cm C. 3cm D. 4cm
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一辆货车从甲地出发以每小时80 km的速度匀速驶往乙地，一段时间后，一辆轿车从乙地出发沿同一条路匀速驶往甲地．货车行驶2.5 h后，在距乙地160 km处与轿车相遇．图中线段AB表示货车离乙地的距离y1 km与货车行驶时间x h的函数关系．
（1）求y1与x之间的函数表达式；
（2）若两车同时到达各自目的地，在同一坐标系中画出轿车离乙地的距离y2与x的图像，求该图像与x轴交点坐标并解释其实际意义．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先化简，再求值：
（1）（2x+y）2﹣y（2x+y），其中x＝
，y＝﹣1；
（2）[（a﹣2b）2+（a﹣2b）（a+2b）﹣2a（2a﹣b）]÷2a，其中a＝3，b＝2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图①∠1＋∠2与∠B＋∠C有什么关系？为什么？
（2）把图①△ABC沿DE折叠，得到图②，填空：∠1＋∠2_______∠B＋∠C(填“＞”“＜”“=”)，当∠A＝40°时，∠B＋∠C＋∠1＋∠2＝______.
（3）如图③,是由图①的△ABC沿DE折叠得到的,如果∠A＝30°,则x＋y＝360°－（∠B＋∠C＋∠1＋∠2）＝360°－ ＝ ,猜想∠BDA＋∠CEA与∠A的关系为
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，点D是边BC的中点，CE∥AB，AD平分∠EAB
(1)延长AD、CE相交于点F，求证:AB＝CE+AE
(2)当点E和点C重合时，试判断△ABC的形状，请画出图形，并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com