
 如图所示,折叠矩形的一边AD,使点D落在边BC的点F处,已知AB=8cm,BC=10cm,则EC的长为3cm.
如图所示,折叠矩形的一边AD,使点D落在边BC的点F处,已知AB=8cm,BC=10cm,则EC的长为3cm. 分析 根据矩形的性质可得AD=BC,CD=AB,再根据翻折变换的性质可得AF=AD,EF=DE,利用勾股定理列式求出BF,再求出CF,设EC=x,表示出EF,然后利用勾股定理列方程求解即可.
解答 解:∵四边形ABCD是矩形,
∴AD=BC=10cm,CD=AB=8cm,
由翻折变换的性质得,AF=AD=10cm,EF=DE,
在Rt△ABF中,根据勾股定理得,BF=$\sqrt{A{F}^{2}-A{B}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6cm,
所以,CF=BC-BF=10-6=4cm,
设EC=x,则EF=DE=(8-x)cm,
在Rt△CEF中,根据勾股定理得,CF2+EC2=EF2,
即42+x2=(8-x)2,
解得x=3cm,
所以,EC的长为3cm.
故答案为:3.
点评 本题考查了翻折变换的性质,翻折前后对应边相等,对应角相等,此类题目,利用勾股定理列出方程是解题的关键.


科目:初中数学 来源: 题型:选择题
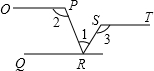 如图,已知OP∥QR∥ST,则下列等式中正确的是( )
如图,已知OP∥QR∥ST,则下列等式中正确的是( )| A. | ∠1+∠2-∠3=90° | B. | ∠1-∠2+∠3=180° | C. | ∠2+∠3-∠1=180° | D. | ∠1+∠2+∠3=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
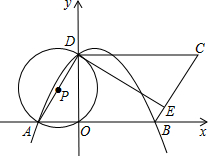 如图,在平面直角坐标系xoy中,O为原点,?ABCD的边AB在x轴上,点D在y轴上,点A的坐标为(-2,0),AB=6,∠BAD=60°,点E是BC边上一点,CE=3EB,⊙P过A、O、D三点,抛物线y=ax2+bx+c过点A、B、D三点.
如图,在平面直角坐标系xoy中,O为原点,?ABCD的边AB在x轴上,点D在y轴上,点A的坐标为(-2,0),AB=6,∠BAD=60°,点E是BC边上一点,CE=3EB,⊙P过A、O、D三点,抛物线y=ax2+bx+c过点A、B、D三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
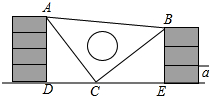 课间,小明拿着老师的等腰直角三角板玩,不小心掉到两墙之间,如图所示.
课间,小明拿着老师的等腰直角三角板玩,不小心掉到两墙之间,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
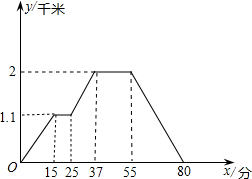 下面的图象反映的过程是:小明从家去超市买文具,又去书店购书,然后回家,其中x表示时间,y表示小明离他家的距离,且小明家、超市、书店在同一直线上.根据图象回答下列问题:
下面的图象反映的过程是:小明从家去超市买文具,又去书店购书,然后回家,其中x表示时间,y表示小明离他家的距离,且小明家、超市、书店在同一直线上.根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +8 | -2 | -3 | +16 | -9 | +10 | -11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com