
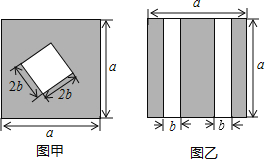
【题目】为打造美丽校园,小明、小红为校园内的一块空地分别提供了如图甲、乙的设计方案,其中阴影部分都用于绿化,图甲空白区域修建一座雕像,图乙空白区域修建石子小路.已知S甲表示图甲中绿化的面积S乙表示图乙中绿化的面积.
(1)S甲= (用含a,b的代数式表示);
(2)设k=![]() ,
,
①请用含a,b的代数式表示k并化简;
②当2S甲﹣S乙=![]() a2时,求k的值.
a2时,求k的值.
 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】(本题满分12分)快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速继续向甲地行驶,到达甲地后停止行驶;快车到达乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程![]() (千米)与所用时间
(千米)与所用时间![]() (小时)之间的函数图象如图,请结合图象信息解答下列问题:
(小时)之间的函数图象如图,请结合图象信息解答下列问题:
(1)求慢车的行驶速度和![]() 的值;
的值;
(2)求快车与慢车第一次相遇时,距离甲地的路程是多少千米?
(3)求两车出发后几小时相距的路程为![]() 千米?
千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA的方向是北偏东15°,OB的方向是西偏北50°,OD是OB的反向延长线.
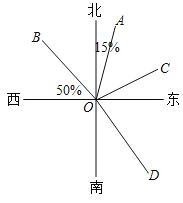
(1)若∠AOC=∠AOB,求OC的方向.
(2)在(1)问的条件下,作∠AOD的角平分线OE,求∠COE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明遇到这样一个问题,如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC.求∠C的度数。小明通过探究发现,延长CD至点Q,使BQ=AB,再证明△ADC≌△ADQ,使问题得到解决.
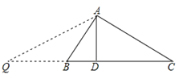
(1)根据阅读材料回答,△ADC≌△ADQ的条件是________(填SSS,SAS,AAS,ASA,或HL)
(2)参考小明思考问题的方法,解答下列问题:求∠C的度数;
(3)解决问题,如图,已知,△ABC中,过点B任意作射线l,在l上取一点D,使∠ABD=∠ACD,AM⊥BD于点M,且BM=MD+CD。探究AB与AC的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD,AB=6,AD=8,将矩形ABCD绕点A顺时针旋转θ(0°<θ<360°)得到矩形AEFG,当θ=_____°时,GC=GB.
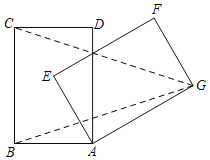
查看答案和解析>>
科目:初中数学 来源: 题型:
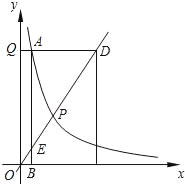
【题目】如图,已知正比例函数的图象与反比例函数的图象都经过点P(2,3),点D是正比例函数图象上的一点,过点D作y轴的垂线,垂足分别Q,DQ交反比例函数的图象于点A,过点A作x轴的垂线,垂足为B,AB交正比例函数的图于点E.
(1)求正比例函数解析式、反比例函数解析式.
(2)当点D的纵坐标为9时,求:点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节约是中华民族的传统美德.为倡导市民节约用水的意识,某市对市民用水实行“阶梯收费”,制定了如下用水收费标准:每户每月的用水不超过![]() 立方米时,水价为每立方米
立方米时,水价为每立方米![]() 元,超过
元,超过![]() 立方米时,超过的部分按每立方米
立方米时,超过的部分按每立方米![]() 元收费.
元收费.
(1)该市某户居民9月份用水![]() 立方米(
立方米(![]() ),应交水费
),应交水费![]() 元,请你用含
元,请你用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)如果某户居民12月份交水费![]() 元,那么这个月该户居民用了多少立方米水?
元,那么这个月该户居民用了多少立方米水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .点
.点![]() 在
在![]() 轴的负半轴上,且
轴的负半轴上,且![]() 的面积为8,直线
的面积为8,直线![]() 和直线
和直线![]() 相交于点
相交于点![]() .
.
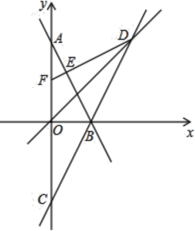
(1)求直线![]() 的解析式;
的解析式;
(2)在线段![]() 上找一点
上找一点![]() ,使得
,使得![]() ,线段
,线段![]() 与
与![]() 相交于点
相交于点![]() .
.
①求点![]() 的坐标;
的坐标;
②点![]() 在
在![]() 轴上,且
轴上,且![]() ,直接写出
,直接写出![]() 的长为 .
的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin65°≈
,sin65°≈![]() ,tan65°≈
,tan65°≈![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com