
分析 (1)分子分母同时乘以($\sqrt{23}$-$\sqrt{22}$)进行化简;
(2)先利用上题的规律将每一个分数化为两个二次根式的差的形式,再计算即可.
解答 解:(1)原式=$\frac{\sqrt{23}-\sqrt{22}}{(\sqrt{23}+\sqrt{22})(\sqrt{23}-\sqrt{22})}$=$\sqrt{23}$-$\sqrt{22}$;
故答案是:$\sqrt{23}$-$\sqrt{22}$;
(2)$\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+2}$+…+$\frac{1}{\sqrt{99}+\sqrt{100}}$,
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+2-$\sqrt{3}$+…+$\sqrt{100}$-$\sqrt{99}$
=$\sqrt{100}$-1
=9.
点评 此题的关键是分母有理化,得出规律:$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在菱形ABCD中,∠BAD=60°,M为对角线BD延长线上一点,连接AM和CM,E为CM上一点,且满足CB=CE,连接BE,交CD于点F.
如图,在菱形ABCD中,∠BAD=60°,M为对角线BD延长线上一点,连接AM和CM,E为CM上一点,且满足CB=CE,连接BE,交CD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
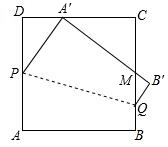 如图,将一块边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点A′,使DA′=5,折痕为PQ,
如图,将一块边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点A′,使DA′=5,折痕为PQ,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲 | 乙 | 丙 | |
| 平均货轮载重的吨数(万吨) | 10 | 5 | 7.5 |
| 平均每吨货物可获例如(百元) | 5 | 3.6 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
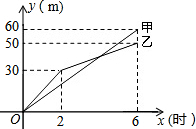 某市在一次市政施工中,有两段长度相等的人行道铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设人行道的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
某市在一次市政施工中,有两段长度相等的人行道铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设人行道的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com