
����Ŀ����֪��������ABCD�У�AD��BC����A=90�㣬AD=2��AB=4��BC=5��������BC��ȡһ��M������DM������MDN=��BDC����MDN����һ��DN��ֱ��BC�ڵ�N����N�ڵ�M����ࣩ��
��1����BM�ij�Ϊ10ʱ����֤��BD��DM��
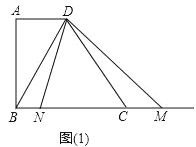
��2����ͼ��1��������N���߶�BC��ʱ����BN=x��BM=y����y����x�ĺ�����ϵʽ����д�����Ķ�����
��3�������DMN�ǵ��������Σ���BN�ij���

���𰸡���1������������2��y=![]() ��0��x��4����3��BN=0��1��2
��0��x��4����3��BN=0��1��2![]() ��4��
��4��
�����������������
��1����ͼ1������D��DG��BC��G������֪���ı���ABGD�Ǿ��Σ���BG=AD=2��DG=AB=4����BC=5�ɵ�CG=3���ɹ��ɶ����ɵ�CD=5�����BM=10�ɵ�CM=BM-BC=5=BC=CD���ɴ˿ɵá�BDM��ֱ�������Σ��Ӷ��ɵ�BD��DM��
��2����ͼ1���ɣ�1����CD==5=BC�ɵá�BDC=��DBC��ϡ�MDN=��BDC���ɵõ���DBC=��MDN���ٽ�ϡ�BMD=��DMN�ɵá�MDN�ס�MBD���Ӷ��ɵ�DM2=BM��MN���DM2=DG2+MG2=16+��y��2��2��MN=BM��BN=y��x���ɵ�16+��y��2��2=y��y��x���������ɵ�y=![]() ����ϵ�N���߶�BC�Ͽɵ�x��ȡֵ��Χ�ǣ�
����ϵ�N���߶�BC�Ͽɵ�x��ȡֵ��Χ�ǣ�![]() ��
��
��3���֣���DN=DM��II��DM=MN��III��MN=DN������������֪������ǰ�����ý��۽��з������㼴��.
���������
��1����ͼ1������D��DG��BC��G��
���BGD=90�㣬
�ߡ�A=90�㣬����ABCD�У�AD��BC��
���ABC=90�㣬
���ı���ABGD�Ǿ��Σ�BG=AD=2��DG=AB=4��
��BC=5��
��CG=BC��BG=3��
��Rt��CDG�У����ݹ��ɶ����ã�CD=5��
��BM=10��
��CM=BM��BC=5=BC=CD��
���BDM��ֱ�������Σ�
��BD��DM��
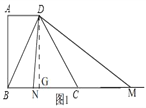
��2���ɣ�1��֪��CD=5=BC��
���BDC=��DBC��
�ߡ�MDN=��BDC��
���DBC=��MDN��
�ߡ�BMD=��DMN��
���MDN�ס�MBD��
��![]() ��
��
��DM2=BM��MN
��Rt��DMG�У����ݹ��ɶ����ã�DM2=DG2+MG2=16+��y��2��2��
��MN=BM��BN=y��x��
��16+��y��2��2=y��y��x����
��y=![]() ��
��
�֡ߵ�N���߶�BC�ϣ�
��0��x��4��
��3���ߡ�DMN�ǵ��������Σ�
��������DN=DMʱ����ͼ1��NG=MG��
��NG=2��x��MG=y��2��
��2��x=y��2��
��x+y=4����
�ɣ�2��֪��y=![]() ��
��
��y��4��x��=20��
�����٢ڣ����x=��![]() ��4���ᣩ��x=
��4���ᣩ��x=![]() ��4��
��4��
����BN=![]() -4��
-4��
������DM=MNʱ��
���MDN=��DNM��
�ߡ�CBD=��MDN��
���CBD=��DNM��
���N���B�غϣ�
��BN=0��
������MN=DNʱ��
���MDN=��DMN��
�ߡ�DBC=��MDN��
���DBC=��DMN��
��DM=BD��
��Rt��ABD�У����ݹ��ɶ����ã�BD/span>2=AD2+AB2=20��
��DM2=16+��BM��2��2��
��20=16+��BM��2��2��
��BM=0����ȥ����BM=4��
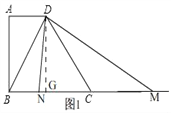
����ͼ2��
��M���߶�BC�ϣ�
ͬ��2���ķ����ã�16+��BM��2��2=BM��BM��BN������
��MN=BN+BM����
�����ۢܽ�ã�BN=1��
����BN=0��1��![]() ��4��
��4��


 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д� Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д� ״Ԫ����ϵ�д�
״Ԫ����ϵ�д� ͬ������ϵ�д�
ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧϰ��һ�κ�����ijУ��ѧ��ȤС�����ѧϰ�ľ��飬�Ժ���y=-��x��-2��ͼ������ʽ�����̽���������Ǹ���ȤС���̽�����̣��벹������:
(1)�Ա���x��ȡֵ��Χ��ȫ��ʵ����x��y�ļ����Ӧֵ���:
x | ... | -3 | -2 | -1 | 0 | 1 | 2 | 3 | ... |
y | ... | -5 | -4 | -3 | n | -3 | -4 | -5 | ... |
��n= ��
����ͼ����������ƽ��ֱ������ϵ�У�����Ա��и����ӦֵΪ����ĵ㣬��������ĵ㻭���ú�����ͼ��

(2)��һ2��x��5ʱ��y��ȡֵ��Χ�� ��
(3)����������ͼ����д��һ�����ڸú���ͼ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�������߳��ֱ�Ϊ2��5��6������ABC����ƽ���ڻ�һ��ֱ�ߣ�����ABC�ֳ����������Σ�ʹ����һ��������Ϊ����������.

��1��������ֱ�������Ի� ����
��2��������������ͼ�зֱ�����������һ��ֱ�ߣ�Ҫ��ÿ��ͼ�еõ��ĵ���������������ͬ���߹���ͼ����д������������ͼ�ۼ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ף�����ƽ���ϲ�����90��ġ�MON�����Ǹ������¶��壺�����P�ڡ�MON���ڲ�����PE��OM��PF��ON������ֱ�Ϊ��E��F����ô��PE+PF��ֵΪ��P����ڡ�MON�ġ���Ǿ��롱����Ϊd��P����MON������ͼ�ң���ƽ��ֱ������ϵxOy�У���P������ƽ���ڣ��ҵ�P�ĺ�������������2�����ڡ�xOy������d��P����xOy��=10����P��������_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����л���ͳ�Ļ���ǭ���ݽ��ھٰ�����Сѧ������ѧ�����������������ĿΪ��A����ʫ��B���δʣ�C�����D�����־���������ʽ����������������˫��������
��1��С���μ������������������������ȡһ��������Ŀ��ǡ�ó��������־����ĸ����Ƕ��٣�
��2��С���С�����һ��С��μ���˫���������������������ǣ�ͬһС���������Ա�ı�����Ŀ������ͬ����ÿ��ֻ�������ȡһ�Σ���ǡ��С���������ʫ����С���������δ����ĸ����Ƕ��٣����û���״ͼ���б��ķ�������˵����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��Ӧ����ɫ�������ĺ��٣�С���ϰ����Լݳ���Ϊ����������.��֪С���Ҿ����ϰ�ص�![]() ��������������ƽ��ÿСʱ��ʻ��·�̱����Լݳ�ƽ��ÿСʱ��ʻ��·�̵�
��������������ƽ��ÿСʱ��ʻ��·�̱����Լݳ�ƽ��ÿСʱ��ʻ��·�̵�![]() ������
������![]() .���Ӽҳ������ϰ�ص㣬�˹��������õ�ʱ�����Լݳ�����ʱ���
.���Ӽҳ������ϰ�ص㣬�˹��������õ�ʱ�����Լݳ�����ʱ���![]() .
.
��1��С�����Լݳ��ϰ�ƽ��ÿСʱ��ʻ����ǧ�ף�
��2�������壬С���ϰ�ʱ�Ȳ�����![]() ��Ȼ��˹�����ǰ��������
��Ȼ��˹�����ǰ��������![]() Сʱ����.�������е��ٶ�.
Сʱ����.�������е��ٶ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y1=![]() ��x+1��2+1��y2=a��x��4��2��3���ڵ�A��1��3��������A��x���ƽ���ߣ��ֱ�������������B��C���㣬��D��E�ֱ�Ϊ���㣮�����н��ۣ���a=
��x+1��2+1��y2=a��x��4��2��3���ڵ�A��1��3��������A��x���ƽ���ߣ��ֱ�������������B��C���㣬��D��E�ֱ�Ϊ���㣮�����н��ۣ���a=![]() ����AC=AE���ۡ�ABD�ǵ���ֱ�������Σ��ܵ�x��1ʱ��y1��y2�� ������ȷ���۵ĸ����ǣ� )
����AC=AE���ۡ�ABD�ǵ���ֱ�������Σ��ܵ�x��1ʱ��y1��y2�� ������ȷ���۵ĸ����ǣ� )

A. 1��B��2��C��3��D��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ľ��˾��20��������һ�������������У��ù�˾���ʻ���������������y1(���)��ʱ��x(xΪ����,��λ:��)���ֶ�Ӧֵ���±���ʾ��
ʱ��x���죩 | 0 | 4 | 8 | 12 | 16 | 20 |
����y1(���) | 0 | 16 | 24 | 24 | 16 | 0 |
��һ�����ʻ����Ա������ۣ�����������������y2(���)��ʱ��x(xΪ����,��λ:��) ��ϵ����ͼ��ʾ��

��1���������ѧ����һ�κ��������κ����ͷ�����������ȷ�����ֺ����ܱ�ʾy1��x�ı仯���ɣ�д��y1��x�ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
��2���۲�����������������y2��ʱ��x�ı仯���ɣ����������̼Ҳ����˺������۲���ʹ�������������˱仯����д��������y2��x�ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
��3����û�ľ��˾����������Ϊy��䣬д��y��ʱ��x�ĺ�����ϵʽ�����жϵڼ�������������y��������ʱ���ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳���3��BP=CQ������AQ��DP���ڵ�O�����ֱ����CD��BC���ڵ�F��E������AE�����н��ۣ���AQ��DP����OA2=OEOP����S��AOD=S�ı���OECF���ܵ�BP=1ʱ��tan��OAE=![]() ��������ȷ���۵ĸ����ǣ�������
��������ȷ���۵ĸ����ǣ�������

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com