
���� ��1���ô���ϵ������������ߵĽ���ʽ�������䷽������Գ���Ͷ������ꣻ
��2���������ɵ�E��4-m��n����F��m-4��n�����Ӷ��õ�PF=4�����ı���OAPF�����Ϊ48�������P�������꣬Ȼ����������ߵĽ���ʽ�Ϳ������P�����꣮
��3���ɵ�E���P����ֱ��l�Գƿɵ�MP=ME������MP+MA=ME+MA�����ݡ�����֮���߶���̡��ɵ�AE�ij�����MP+MA����Сֵ��ֻ�����ù��ɶ����Ϳɽ�����⣮
��� �⣩��������y=x2+bx+c����A��4��0����B��1��-3����
��$\left\{\begin{array}{l}{16+4b+c=0}\\{1+b+c=-3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{b=-4}\\{c=0}\end{array}\right.$��
��y=x2-4x=��x-2��2-4��
�������ߵĶԳ���Ϊx=2������Ϊ��2��-4����
��2����ͼ1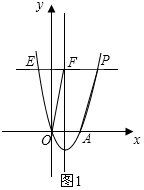 ��
��
�ߵ�P��m��n�����E����ֱ��x=2�Գƣ�
���E��������4-m��n����
�ߵ�E���F����y��Գƣ�
���F��������m-4��n����
��PF=m-��m-4��=4��
��PF=OA=4��
��PF��OA��
���ı���OAPF��ƽ���ı��Σ�
��S?OAPF=OA•|yP|=4n=15��
��n=$\frac{15}{4}$��
��m2-4m=n=$\frac{15}{4}$��
��ã�m1=$\frac{4+\sqrt{31}}{2}$��m2=$\frac{4-\sqrt{31}}{2}$��
�ߵ�P�����������ڵ�һ�����ڵĵ㣬
��m=$\frac{4+\sqrt{31}}{2}$��
���P��������$\frac{4+\sqrt{31}}{2}$��$\frac{15}{4}$����
��3������E��EH��x�ᣬ����ΪH����ͼ2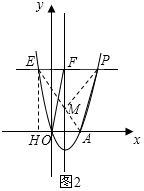 ��
��
�ڣ�2���������£���P��$\frac{4+\sqrt{31}}{2}$��$\frac{15}{4}$����E��$\frac{-4-\sqrt{31}}{2}$��$\frac{15}{4}$����
��AH=4-��$\frac{-4-\sqrt{31}}{2}$��=$\frac{12+\sqrt{31}}{2}$��EH=$\frac{15}{4}$��
��EH��x�ᣬ����EHA=90�㣬
��EA2=EH2+AH2=��$\frac{15}{4}$��2+��$\frac{12+\sqrt{31}}{2}$��2=$\frac{925+96\sqrt{31}}{16}$��
��EA=$\frac{\sqrt{925+96\sqrt{31}}}{4}$��
�ߵ�E���P����ֱ��l�Գƣ�
��MP=ME��
��MP+MA=ME+MA��
���ݡ�����֮���߶���̡��ɵã�
����E��M��A����ʱ��MP+MA��С����Сֵ����EA�ij�����$\frac{\sqrt{925+96\sqrt{31}}}{4}$��
��ֱ��AE�Ľ���ʽΪy=mx+n��
��$\left\{\begin{array}{l}{\frac{-4-\sqrt{31}}{2}m+n=\frac{15}{4}}\\{4m+n=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{m=\frac{-186+\sqrt{31}}{113}}\\{n=\frac{744-4\sqrt{31}}{113}}\end{array}\right.$��
��ֱ��AE�Ľ���ʽΪy=$\frac{-118+\sqrt{31}}{113}$x+$\frac{744-4\sqrt{31}}{113}$��
��x=2ʱ��y=$\frac{508-2\sqrt{31}}{113}$�����M������Ϊ��2��$\frac{508-2\sqrt{31}}{113}$����
��MP+MAȡ����Сֵ����СֵΪ$\frac{\sqrt{925+96\sqrt{31}}}{4}$������ʱ��Ӧ��M������Ϊ��2��$\frac{508-2\sqrt{31}}{113}$����
���� ���⿼�����ô���ϵ��������κ�����һ�κ����Ľ���ʽ������֮���߶���̡����ɶ�������һԪ���η��̡�ƽ���ı��ε��ж������ʡ����������߶Գ���ԳƼ�����y��ԳƵ������������֪ʶ����һ�����ۺ��ԣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
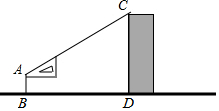 ��ͼ��С�����ú�30��ǵ����ǰ����¥���߶ȵ�ʾ��ͼ����֪���Ӹ�ABΪ1�ף�������B��D֮��ľ���Ϊ100�ף���¥��CDԼΪ��������
��ͼ��С�����ú�30��ǵ����ǰ����¥���߶ȵ�ʾ��ͼ����֪���Ӹ�ABΪ1�ף�������B��D֮��ľ���Ϊ100�ף���¥��CDԼΪ��������| A�� | 51�� | B�� | 59�� | C�� | 88�� | D�� | 174�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
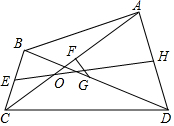 ��ͼ����֪���ı���ABCD�У�E��F��G��H�ֱ�ΪBC��AC��BD��AD���е㣮��֤��EH��FG����ƽ�֣�
��ͼ����֪���ı���ABCD�У�E��F��G��H�ֱ�ΪBC��AC��BD��AD���е㣮��֤��EH��FG����ƽ�֣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
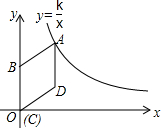 ��ͼ������ABCD�Ķ���C��ԭ��O�غϣ���B��y����������ϣ���A�ڷ���������y=$\frac{k}{x}$��k��0��x��0����ͼ���ϣ���D������Ϊ��4��3������k��ֵΪ32��
��ͼ������ABCD�Ķ���C��ԭ��O�غϣ���B��y����������ϣ���A�ڷ���������y=$\frac{k}{x}$��k��0��x��0����ͼ���ϣ���D������Ϊ��4��3������k��ֵΪ32���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com