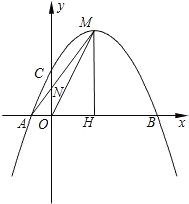
在平面直角坐标系xOy中,O是坐标原点,等边三角形OAB的一个顶点为A(2,0),另一个顶点B在第一象限内.
(1)求经过O、A、B三点的抛物线的解析式;
(2)如果一个四边形是以它的一条对角线为对称轴的轴对称图形,那么我们称这样的四边形为“筝形”.点Q在(1)的抛物线上,且以O、A、B、Q为顶点的四边形是“筝形”,求点Q的坐标;
(3)设△OAB的外接圆⊙M,试判断(2)中的点Q与⊙M的位置关系,并通过计算说明理由.
解:(1)过B作BC⊥x轴于C.
∵等边三角形OAB的一个顶点为A(2,0),

∴OB=OA=2,AC=OC=1,∠BOC=60°.
∴BC=
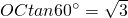
.
∴B

.
设经过O、A、B三点的抛物线的
解析式为:
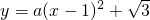
.
将A(2,0)代入得:
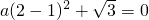
,
解得
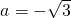
.
∴经过O、A、B三点的抛物线的解析式为
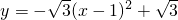
.
即
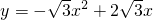
;
(2)依题意分为三种情况:
(ⅰ)当以OA、OB为边时,
∵OA=OB,
∴过O作OQ⊥AB交抛物线于Q.
则四边形OAQB是筝形,且∠QOA=30°.
作QD⊥x轴于D,QD=ODtan∠QOD,
设Q
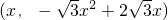
,则
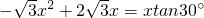
.
解得:

.
∴Q
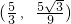
.
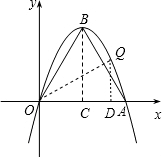
(ⅱ)当以OA、AB为边时,由对称性可知Q
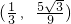
.
(ⅲ)当以OB、AB为边时,抛物线上不存在这样的点Q使BOQA为筝形.
∴Q
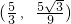
或
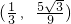
.
(3)点Q在⊙M内.
由等边三角形性质可知△OAB的外接圆圆心M是(2)中BC与OQ的交点,
当Q
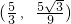
时,
∵MC∥QD,
∴△OMC∽△OQD.
∴

.
∴

.
∴
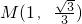
.
∴MQ=
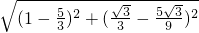
=
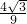
.
又
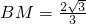
,
∵
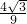
<

,
∴Q
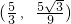
在⊙M内.
当Q
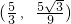
时,由对称性可知点Q在⊙M内.
综述,点Q在⊙M内.
分析:(1)先求出点B,则设抛物线的顶点式,将点A代入即得到方程式;
(2)(ⅰ)当以OA、OB为边时,作QD⊥x轴于D,QD=ODtan∠QOD,QD=ODtan∠QOD,从而求得点Q.(ⅱ)当以OA、AB为边时,由对称性求得Q.(ⅲ)当以OB、AB为边时,抛物线上不存在这样的点Q使BOQA为筝形.求得点Q.
(3)点Q在⊙M内.由等边三角形性质可知△OAB的外接圆圆心M是(2)中BC与OQ的交点,求得△OMC∽△OQD.从而求得点M,进而求得MQ,从而求得点Q的位置.
点评:本题考查了二次函数的综合运用,(1)先求出点B,则设抛物线的顶点式,将点A代入即得到方程式;(2)(ⅰ)当以OA、OB为边时,作QD⊥x轴于D,QD=ODtan∠QOD,QD=ODtan∠QOD,从而求得点Q.(ⅱ)当以OA、AB为边时,由对称性求得Q.(ⅲ)当以OB、AB为边时,抛物线上不存在这样的点Q使BOQA为筝形.求得点Q.(3)点Q在⊙M内.由等边三角形性质可知△OAB的外接圆圆心M是(2)中BC与OQ的交点,求得△OMC∽△OQD.从而求得点M,进而求得MQ,从而求得点Q的位置.本题有一定难度,思路性强.


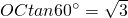 .
. .
.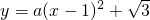 .
.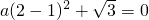 ,
,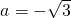 .
.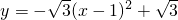 .
.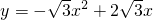 ;
;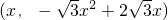 ,则
,则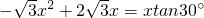 .
. .
.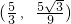 .
.
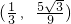 .
.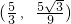 或
或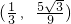 .
.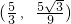 时,
时, .
. .
.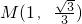 .
.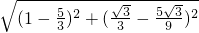 =
=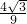 .
.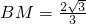 ,
,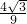 <
< ,
,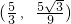 在⊙M内.
在⊙M内. 时,由对称性可知点Q在⊙M内.
时,由对称性可知点Q在⊙M内.

 直线QG的解析式;若不存在,请说明理由.
直线QG的解析式;若不存在,请说明理由.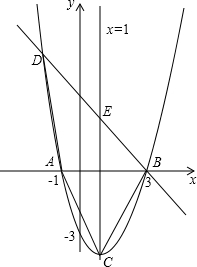 点B在A点的右侧;交y轴于(0,-3).
点B在A点的右侧;交y轴于(0,-3).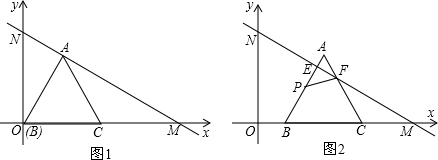
 ,对称轴l与x轴相交于点C,顶点为点D,且∠ADC的正切值为
,对称轴l与x轴相交于点C,顶点为点D,且∠ADC的正切值为 如图①,在等腰直角三角板ABC中,斜边BC为2个单位长度,现把这块三角板在平面直角坐标系xOy中滑动,并使B、C两点始终分别位于y轴、x轴的正半轴上,直角顶点A与原点O位于BC两侧.
如图①,在等腰直角三角板ABC中,斜边BC为2个单位长度,现把这块三角板在平面直角坐标系xOy中滑动,并使B、C两点始终分别位于y轴、x轴的正半轴上,直角顶点A与原点O位于BC两侧.