
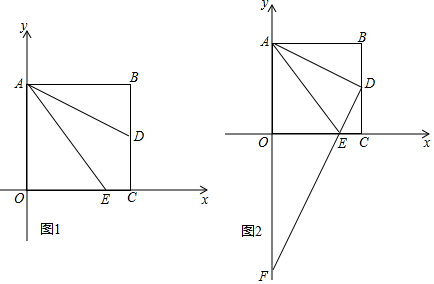
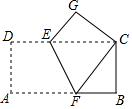
·ÖĪö £Ø1£©øł¾Ż¶ž“ĪøłŹ½µÄŠŌÖŹ£ŗ±»æŖ·½ŹżŹĒ·ĒøŗŹż£¬ĮŠ³ö²»µČŹ½¼“æɽā¾öĪŹĢā£»
£Ø2£©Ź×ĻČÖ¤Ć÷ĖıߊĪABCOŹĒÕż·½ŠĪ£¬ŃÓ³¤COµ½M£¬Ź¹µĆOM=BD£¬Ōņ”÷ABD”Õ”÷AOM£¬Ö»ŅŖÖ¤Ć÷”ĻM=”ĻEAM£¬¼“æÉĶĘ³öAE=EM=OE+OM=OE+BD£»
£Ø3£©ČēĶ¼2ÖŠ£¬ÉčAE=EM=x£®ŌŚRt”÷OAEÖŠ£¬ĄūÓĆ¹“¹É¶ØĄķĮŠ³ö·½³Ģ£¬Ēó³öµćE×ų±ź£¬ĄūÓĆ“ż¶ØĻµŹż·ØĒó³öÖ±ĻßDEµÄ½āĪöŹ½¼“æɽā¾öĪŹĢā£»
½ā“š ½ā£ŗ£Ø1£©”ßĒŅ$\sqrt{2a-8\sqrt{5}}$+$\sqrt{4\sqrt{5}-a}$+2$\sqrt{5}$=b£¬
”ą2a-8$\sqrt{5}$”Ż0ĒŅ4$\sqrt{5}$-a”Ż0£¬
”ąa”Ż4$\sqrt{5}$ĒŅa$”Ü4\sqrt{5}$£¬
”ąa=4$\sqrt{5}$£¬b=2$\sqrt{5}$£¬
¹Ź“š°øĪŖ4$\sqrt{5}$£¬2$\sqrt{5}$£®
£Ø2£©ÓÉ£Ø1£©æÉÖŖAB=4$\sqrt{5}$£¬CD=BD=2$\sqrt{5}$£¬
”ąAB=CD£¬
”ßAB”ĶyÖįÓŚµćA£¬BC”ĶxÖįÓŚµćB£¬
”ą”ĻBAO=”ĻB=”ĻAOC=90”ć£¬
”ąĖıߊĪABCOŹĒ¾ŲŠĪ£¬”ßAB=CD£¬
”ąĖıߊĪABCOŹĒÕż·½ŠĪ£¬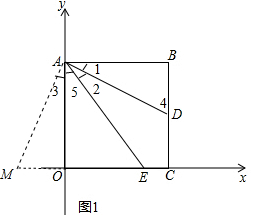
ŃÓ³¤COµ½M£¬Ź¹µĆOM=BD£¬Ōņ”÷ABD”Õ”÷AOM£¬
”ą”Ļ4=”ĻM£¬”Ļ1=”Ļ2=”Ļ3£¬
”ßOA”ĪBC£¬
”ą”Ļ4=”Ļ2+”Ļ5=”Ļ5+”Ļ3=”ĻEAM£¬
”ą”ĻM=”ĻEAM£¬
”ąAE=EM=OE+OM=OE+BD£®
£Ø3£©ČēĶ¼2ÖŠ£¬ÉčAE=EM=x£®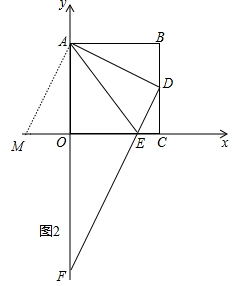
ŌŚRt”÷AOEÖŠ£¬”ßAO2=OE2=AE2£¬
”ąx2=£Ø4$\sqrt{5}$£©2+£Øx-2$\sqrt{5}$£©2£¬
”ąx=5$\sqrt{3}$£¬
”ąOE=3$\sqrt{5}$£¬
”ąD£Ø4$\sqrt{5}$£¬2$\sqrt{5}$£©£¬E£Ø3$\sqrt{5}$£¬0£©£¬
ÉčÖ±ĻßDEµÄ½āĪöŹ½ĪŖy=kx+b£¬ŌņÓŠ$\left\{\begin{array}{l}{4\sqrt{5}k+b=2\sqrt{5}}\\{3\sqrt{5}k+b=0}\end{array}\right.$£¬
½āµĆ$\left\{\begin{array}{l}{k=2}\\{b=-6\sqrt{5}}\end{array}\right.$£¬
”ąÖ±ĻßDEµÄ½āĪöŹ½ĪŖy=2x-6$\sqrt{6}$£¬
”ąF£Ø0£¬-6$\sqrt{5}$£©
µćĘĄ ±¾Ģāæ¼²éČż½ĒŠĪ×ŪŗĻĢā”¢Õż·½ŠĪµÄÅŠ¶ØŗĶŠŌÖŹ”¢Ņ»“ĪŗÆŹżµÄÓ¦ÓĆ”¢Č«µČČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹ”¢¹“¹É¶ØĄķ£®µČŃüČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹ”¢¶ž“ĪøłŹ½µÄŠŌÖŹµČÖŖŹ¶£¬½āĢāµÄ¹Ų¼üŹĒѧ»įĢķ¼Ó³£ÓĆøØÖśĻߣ¬¹¹ŌģČ«µČČż½ĒŠĪ½ā¾öĪŹĢā£¬Ń§»įĄūÓĆ²ĪŹż¹¹½Ø·½³Ģ½ā¾öĪŹĢā£¬ŹōÓŚÖŠæ¼Ń¹ÖįĢā£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ČēĶ¼£¬ŌŚ?ABCDÖŠ£¬E”¢F·Ö±šŹĒAD”¢CBÉĻČĪŅ»µć£¬AE”ŁCF£¬AB=8£¬CB=10£¬S”÷BOE=6£»ŌņS”÷DOF=6£®
ČēĶ¼£¬ŌŚ?ABCDÖŠ£¬E”¢F·Ö±šŹĒAD”¢CBÉĻČĪŅ»µć£¬AE”ŁCF£¬AB=8£¬CB=10£¬S”÷BOE=6£»ŌņS”÷DOF=6£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
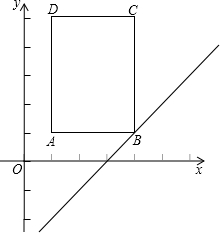 ČēĶ¼£¬¾ŲŠĪABCDŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćA£Ø1£¬1£©£¬B£Ø4£¬1£©£¬C£Ø4£¬5£©£¬D£Ø1£¬5£©£¬½«Ņ»“ĪŗÆŹży=x-3µÄĶ¼ĻóLŃŲyÖįŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČĻņÉĻŌĖ¶Æ£¬ÉčŌĖ¶ÆµÄŹ±¼äĪŖtĆė£¬LÉعż¾ŲŠĪµÄĆ껿ĪŖS£®
ČēĶ¼£¬¾ŲŠĪABCDŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćA£Ø1£¬1£©£¬B£Ø4£¬1£©£¬C£Ø4£¬5£©£¬D£Ø1£¬5£©£¬½«Ņ»“ĪŗÆŹży=x-3µÄĶ¼ĻóLŃŲyÖįŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČĻņÉĻŌĖ¶Æ£¬ÉčŌĖ¶ÆµÄŹ±¼äĪŖtĆė£¬LÉعż¾ŲŠĪµÄĆ껿ĪŖS£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
 ČēĶ¼ŹĒ¶ž“ĪŗÆŹży=ax2+bx+cĶ¼ĻóµÄŅ»²æ·Ö£¬ĒŅ¹żµćA£Ø3£¬0£©£¬¶ž“ĪŗÆŹżĶ¼ĻóµÄ¶Ō³ĘÖįŹĒx=1£¬ĻĀĮŠ½įĀŪ£ŗ¢Łb2£¾4ac£»¢Śac£¾0£» ¢Ūa-b+c£¾0£» ¢Ü²»µČŹ½ax2+bx+c£¾0µÄ½ā¼ÆŹĒ-1£¼x£¼3£»¢Żµ±x£¾1Ź±£¬yĖęxµÄŌö“ó¶ų¼õŠ”£¬ĘäÖŠ½įĀŪÕżČ·µÄŠņŗÅŹĒ£Ø””””£©
ČēĶ¼ŹĒ¶ž“ĪŗÆŹży=ax2+bx+cĶ¼ĻóµÄŅ»²æ·Ö£¬ĒŅ¹żµćA£Ø3£¬0£©£¬¶ž“ĪŗÆŹżĶ¼ĻóµÄ¶Ō³ĘÖįŹĒx=1£¬ĻĀĮŠ½įĀŪ£ŗ¢Łb2£¾4ac£»¢Śac£¾0£» ¢Ūa-b+c£¾0£» ¢Ü²»µČŹ½ax2+bx+c£¾0µÄ½ā¼ÆŹĒ-1£¼x£¼3£»¢Żµ±x£¾1Ź±£¬yĖęxµÄŌö“ó¶ų¼õŠ”£¬ĘäÖŠ½įĀŪÕżČ·µÄŠņŗÅŹĒ£Ø””””£©| A£® | ¢Ł¢Ś¢Ū | B£® | ¢Ł¢Ü¢Ż | C£® | ¢Ū¢Ü¢Ż | D£® | ¢Ł¢Ū¢Ż |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬ŅŃÖŖ¾ŲŠĪABCD£¬½«Ö½Ę¬ÕŪµž£¬Ź¹¶„µćAÓėCÖŲŗĻ£¬ÕŪŗŪEF·Ö±šÓŚDC£¬AB½»ÓŚE£¬F£®
ČēĶ¼£¬ŅŃÖŖ¾ŲŠĪABCD£¬½«Ö½Ę¬ÕŪµž£¬Ź¹¶„µćAÓėCÖŲŗĻ£¬ÕŪŗŪEF·Ö±šÓŚDC£¬AB½»ÓŚE£¬F£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 7 | B£® | 5 | C£® | 7»ņ3 | D£® | 3 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 20øö | B£® | 28øö | C£® | 36øö | D£® | 32øö |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | -1 | B£® | 1 | C£® | 0.25 | D£® | 45000 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com