
【题目】在ΔABC中,∠ABC的平分线与∠ACB的外角∠ACE的平分线相交于点D。

⑴.若∠ABC=60°,∠ACB=40°,求∠A和∠D的度数。
⑵.由⑴小题的计算结果,猜想,∠A和∠D有什么数量关系,并加以证明。
【答案】(1)∠A=80°,∠D=40°;(2)∠A=2∠D,理由见解析
【解析】
(1)根据三角形内角和定理,已知∠ABC=60°,∠ACB=40°,易求∠A,根据角平分线定义和外角的性质即可求得∠D度数.
(2)根据三角形内角和定理以及角平分线性质,先求出∠D的等式,再与∠A比较即可解答.
(1)在△ABC中,∠ABC=60°,∠ACB=40°,
∴∠A=180°∠ABC∠ACB=80°,
∵BD为∠ABC,CD为∠ACE的角平分线,
∴∠DBC=![]() ∠ABC=
∠ABC=![]() ×60°=30°,
×60°=30°,
∠ACD=![]() (180°∠ACB)=
(180°∠ACB)=![]() ×140°=70°,
×140°=70°,
∴∠D=180°∠DBC∠ACB∠ACD=180°30°40°70°=40°,
∴∠A=80°,∠D=40°;
(2)通过第(1)的计算,得到∠A=2∠D,理由如下:
∵∠ACE=∠A+∠ABC,
∴∠ACD+∠ECD=∠A+∠ABD+∠DBE,∠DCE=∠D+∠DBC,
又∵BD平分∠ABC,CD平分∠ACE,
∴∠ABD=∠DBE,∠ACD=∠ECD,
∴∠A=2(∠DCE∠DBC),∠D=∠DCE∠DBC,
∴∠A=2∠D.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】观察下列多面体,并把下表补充完整.
名称 | 三棱柱 | 四棱柱 | 五棱柱 | 六棱柱 |
图形 |
|
|
|
|
顶点数 | 6 | 10 | 12 | |
棱数 | 9 | 12 | ||
面数 | 5 | 8 |
观察上表中的结果,你能发现![]() 、
、![]() 、
、之间有什么关系吗?请写出关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
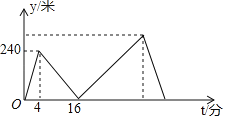
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟.在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t
(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了30分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有320米
其中正确的结论有( )
A. 1 个B. 2 个C. 3 个D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有20个只有颜色不同的球,其中5个黄球,8个黑球,7个红球.
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个黑球的概率是![]() ,求从袋中取出黑球的个数.
,求从袋中取出黑球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D,连接AC,BD,CD.
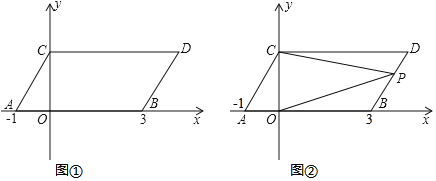
(1)求点C,D的坐标及S四边形ABDC;
(2)在y轴上是否存在一点Q,连接QA,QB,使S△QAB=S四边形ABDC若存在这样一点,求出点Q的坐标;若不存在,试说明理由;
(3)如图②,点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合),求证:∠DCP+∠BOP=∠CPO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A![]() ,B
,B![]() ,且满足
,且满足![]()
(1)求A、B两点的坐标;
(2)点C![]() 在线段AB上,m、n满足n-m=5,点D在y轴负半轴上,连CD交x轴的负半轴于点M,且S△MBC=S△MOD,求点D的坐标;
在线段AB上,m、n满足n-m=5,点D在y轴负半轴上,连CD交x轴的负半轴于点M,且S△MBC=S△MOD,求点D的坐标;
(3)平移直线AB,交x轴正半轴于E,交y轴于F,P为直线EF上第三象限内的点,过P作PG⊥x轴于G,若S△PAB=20,且GE=12,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图),然后将剩余部分拼成一个长方形(如图).

(1)上述操作能验证的等式是 ;(请选择正确的一个)
A.a2-2ab+b2=(a-b)2 B.a2-b2=(a+b)(a-b) C.a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2-4y2=12,x+2y=4,求x-2y的值.
②计算:(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )…(1-
)…(1-![]() )(1-
)(1-![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com