
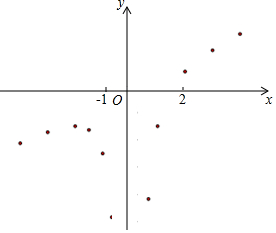
 有这样一个问题:探究函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的图象与性质.
有这样一个问题:探究函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的图象与性质.| x | … | -4 | -3 | -2 | -$\frac{3}{2}$ | -1 | -$\frac{2}{3}$ | $\frac{2}{3}$ | 1 | 2 | 3 | 4 | … |
| y | … | -$\frac{17}{8}$ | -$\frac{31}{18}$ | -$\frac{3}{2}$ | -$\frac{59}{36}$ | -$\frac{5}{2}$ | -$\frac{29}{6}$ | -$\frac{25}{6}$ | -$\frac{3}{2}$ | $\frac{1}{2}$ | $\frac{23}{18}$ | m | … |
分析 (1)由分母不为0,可得出自变量x的取值范围;
(2)将x=4代入函数表达式中,即可求出m值;
(3)连线,画出函数图象;
(4)观察函数图象,找出函数性质.
解答 解:(1)∵x2在分母上,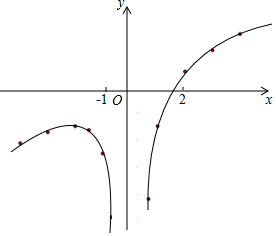
∴x≠0.
故答案为:x≠0.
(2)当x=4时,m=$\frac{1}{2}$x-$\frac{2}{x^2}$=$\frac{1}{2}$×4-$\frac{2}{{4}^{2}}$=$\frac{15}{8}$.
(3)连线,画出函数图象,如图所示.
(4)观察图象,可知:当x>0时,y随x的增大而增大.
故答案为:当x>0时,y随x的增大而增大.
点评 本题考查了分式有意义的条件、二次函数的性质、二次函数的图象以及二次函数的最值,解题的关键是:(1)根据分母不为0,找出x的取值范围;(2)将x=4代入函数关系式求出y值;(3)连点,画出函数图象;(4)根据函数图象,寻找函数的性质.


科目:初中数学 来源: 题型:选择题
| A. | 70°或20° | B. | 55°或45° | C. | 55°或35° | D. | 55°或65° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
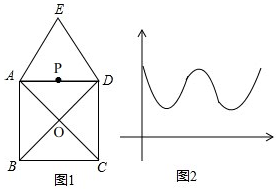
| A. | A→O→D | B. | E→A→C | C. | A→E→D | D. | E→A→B |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB的依据是( )
如图,在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB的依据是( )| A. | SSS | B. | SAS | C. | AAS | D. | HL |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com