
 �ˣ�3����ͬѧ��Ұ������ѧ��Σ�Ϊ������������A��B�ľ��룬��������·�����
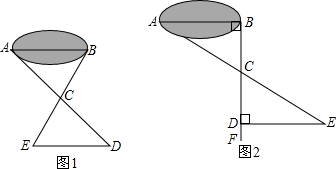
�ˣ�3����ͬѧ��Ұ������ѧ��Σ�Ϊ������������A��B�ľ��룬��������·��������� ��1���������֤����ACB�ա�DCE��AB=DE���ʷ��������У�
��2���������֤����ABC�ա�EDC��AB=ED���ʷ��������У�
��3��������������BF��AB��ED��BF��Ŀ���ǡ�ABD=��BDE�����������ABD=��BDE��90�㣬�ʴ�ʱ��������������
��� �⣺��1�����������У��������£�
��DC=AC��EC=BC��
�ڡ�ACB�͡�DCE�У�$\left\{\begin{array}{l}{AD=DC}&{\;}\\{��ACB=��DCE}&{\;}\\{BC=EC}&{\;}\end{array}\right.$��
���ACB�ա�DCE��SAS����
��AB=DE��
����DE�ľ��뼴ΪAB�ij���
�ʷ��������У�
��2�����������У��������£�
��AB��BC��DE��CD
���ABC=��EDC=90�㣬
�ڡ�ACB�͡�EDC�У�$\left\{\begin{array}{l}{��ABC=��EDC}&{\;}\\{BC=DC}&{\;}\\{��ACB=��ECD}&{\;}\end{array}\right.$��
���ABC�ա�EDC��ASA����
��AB=ED��
����DE�ij���ΪAB�ľ��룬
�ʷ��������У�
��3��������������BF��AB��ED��BF��Ŀ���ǡ�ABD=��BDE��
���������ABD=��BDE��90�㣬��������������
�������£�����ABD=��BDE��90�㣬��ACB=��ECD��
���ABC�ס�EDC��
��$\frac{AB}{ED}=\frac{BC}{CD}$��
��ֻҪ���ED��BC��CD�ij����������AB�ij���
���Ǵ���û��������������������������߶γ��ȣ�
�������������
�ʴ�Ϊ����ABD=��BDE����������
���� �������������ۺ���Ŀ��������ȫ�������ε��ж������ʡ����������ε��ж������ʣ������ۺ���ǿ��֤��������ȫ���ǽ������Ĺؼ���


 ����������ϵ�д�
����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
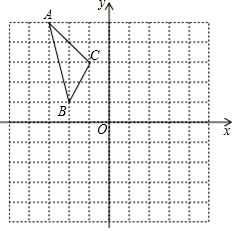 ��ͼ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�ΪA��-3��5����B��-2��1����C��-1��3����
��ͼ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�ΪA��-3��5����B��-2��1����C��-1��3�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�������������Ͻ���ƽ��ֱ������ϵ��ʹ���ڡ�λ�ڵ㣨1��1�������R��λ�ڵ㣨3��-1��������λ�ڵ㣨-2��2����д��������꣩��
��ͼ�������������Ͻ���ƽ��ֱ������ϵ��ʹ���ڡ�λ�ڵ㣨1��1�������R��λ�ڵ㣨3��-1��������λ�ڵ㣨-2��2����д��������꣩���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 3�� | C�� | 5�� | D�� | 7�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
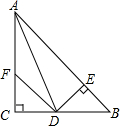 ��ͼ��ʾ���ڡ�ABC�У���C=90�㣬AD�ǡ�BAC��ƽ���ߣ�DE��AB��AB��E��F��AC�ϣ���B=��CFD��
��ͼ��ʾ���ڡ�ABC�У���C=90�㣬AD�ǡ�BAC��ƽ���ߣ�DE��AB��AB��E��F��AC�ϣ���B=��CFD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
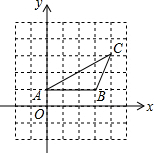 ��֪A��0��1����B��3��1����C��4��3���������ƽ��ֱ������ϵ�д���һ��D��ʹ�á�ABD���ABCȫ�ȣ���ô��D������Ϊ��-1��3����-1��-1����4��-1����
��֪A��0��1����B��3��1����C��4��3���������ƽ��ֱ������ϵ�д���һ��D��ʹ�á�ABD���ABCȫ�ȣ���ô��D������Ϊ��-1��3����-1��-1����4��-1�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com