
【题目】在“长方体、圆柱、圆锥 ”三种几何体中,用一个平面分别去截三种几何体,则截面的形状可以截出长方形也可以截出圆形的几何体是_____.
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
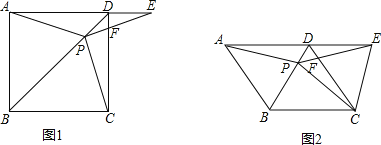
【题目】如图1在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120度时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD,AB=AC,点E,F分别是BC,AD的中点,连接AE,CF.
(1)求证:四边形AECF是矩形;
(2)若AB=8,求菱形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题提出】
学习了三角形全等的判定方法(即“SSS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 ,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角,请你证明:△ABC≌△DEF(提示:过点C作CG⊥AB交AB的延长线于G,过点F作FH⊥DE交DE的延长线于H).
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,请你利用图③,在图③中用尺规作出△DEF,使△DEF和△ABC不全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若x0是方程ax2+2x+c=0(a≠0)的一个根,设M=1﹣ac,N=(ax0+1)2 , 则M与N的大小关系正确的为( )
A.M>N
B.M=N
C.M<N
D.不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明爸爸经营的水果店出售一种优质热带水果,正在上初三的小明经过调查和计算,发现这种水果每月的销售量y(千克)与销售单价x(元)之间存在着一次函数关系:y=-10x+500(20≤x≤50).下面是他们的一次对话:
小明:“您要是告诉我咱家这种水果的进价是多少?我就能帮你预测好多信息呢!”
爸爸:“咱家这种水果的进价是每千克20元”
聪明的你,也来解答一下小明想要解决的两个问题:
(1)若每月获得利润w(元)是销售单价x(元)的函数,求这个函数的表达式.
(2)当销售单价为多少元时,每月可获得最大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com