
”¾ĢāÄæ”æĻČŌĶĮ²ÄĮĻ£ŗČēĶ¼(1),ŌŚŹżÖįÉĻµć![]() Ź¾µÄŹżĪŖ
Ź¾µÄŹżĪŖ![]() µć±ķŹ¾µÄŹżĪŖ
µć±ķŹ¾µÄŹżĪŖ![]() ,Ōņµć
,Ōņµć![]() µ½µć
µ½µć![]() µÄ¾ąĄė¼ĒĪŖ
µÄ¾ąĄė¼ĒĪŖ![]() ,Ļ߶Ī
,Ļ߶Ī![]() µÄ³¤æÉŅŌÓĆÓŅ±ßµÄŹż¼õČ„×ó±ßµÄŹż±ķŹ¾,¼“
µÄ³¤æÉŅŌÓĆÓŅ±ßµÄŹż¼õČ„×ó±ßµÄŹż±ķŹ¾,¼“![]()
![]()
½ā¾öĪŹĢā£ŗČēĶ¼(2),ŹżÖįÉĻµć![]() ±ķŹ¾µÄŹżŹĒ
±ķŹ¾µÄŹżŹĒ![]() ,µć
,µć![]() ±ķŹ¾µÄŹżŹĒ
±ķŹ¾µÄŹżŹĒ![]() ,ĒŅÓŠ
,ĒŅÓŠ![]() £¬µć
£¬µć![]() ±ķŹ¾µÄŹżŹĒ
±ķŹ¾µÄŹżŹĒ![]() £®
£®
![]()
(1)ČōŹżÖįÉĻÓŠŅ»µć![]() ,ĒŅ
,ĒŅ![]() ,Ōņµć
,Ōņµć![]() ±ķŹ¾µÄŹżĪŖ______.
±ķŹ¾µÄŹżĪŖ______.
(2)Čōµć![]() ŅŌĆæĆė
ŅŌĆæĆė![]() øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņ×óŌĖ¶Æµ½
øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņ×óŌĖ¶Æµ½![]() ,Ķ¬Ź±µć
,Ķ¬Ź±µć![]() ŗĶµć
ŗĶµć![]() ·Ö±šŅŌĆæĆė
·Ö±šŅŌĆæĆė![]() øöµ„Ī»³¤¶ČŗĶ
øöµ„Ī»³¤¶ČŗĶ![]() øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņÓŅŌĖ¶Æ·Ö±šµ½
øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņÓŅŌĖ¶Æ·Ö±šµ½![]() ,¼ŁÉč
,¼ŁÉč![]() ĆėÖÓ¹żŗó,Čōµć
ĆėÖÓ¹żŗó,Čōµć![]() Óėµć
Óėµć![]() Ö®¼äµÄ¾ąĄė±ķŹ¾ĪŖ
Ö®¼äµÄ¾ąĄė±ķŹ¾ĪŖ![]() ,µć
,µć![]() Óėµć
Óėµć![]() Ö®¼äµÄ¾ąĄė±ķŹ¾ĪŖ
Ö®¼äµÄ¾ąĄė±ķŹ¾ĪŖ![]() ,µć
,µć![]() Óėµć
Óėµć![]() Ö®¼äµÄ¾ąĄė±ķŹ¾ĪŖ
Ö®¼äµÄ¾ąĄė±ķŹ¾ĪŖ![]() £®Ōņµć
£®Ōņµć![]() ±ķŹ¾µÄŹżŹĒ______,
±ķŹ¾µÄŹżŹĒ______,![]() =________
=________![]() ÓĆŗ¬
ÓĆŗ¬![]() µÄŹ½×Ó±ķŹ¾
µÄŹ½×Ó±ķŹ¾![]() £®
£®
(3)ĒėĪŹ£ŗ![]() µÄÖµŹĒ·ńĖę×ÅŹ±¼ä
µÄÖµŹĒ·ńĖę×ÅŹ±¼ä![]() µÄ±ä»Æ¶ųøıä£æČō±ä»Æ,ĒėĖµĆ÷ĄķÓÉ£»Čō²»±ä,ĒėĒóĘäÖµ.
µÄ±ä»Æ¶ųøıä£æČō±ä»Æ,ĒėĖµĆ÷ĄķÓÉ£»Čō²»±ä,ĒėĒóĘäÖµ.
(4)Čōµć![]() µć
µć![]() ·Ö±šŅŌ
·Ö±šŅŌ![]() øöµ„Ī»ĆæĆėŗĶ
øöµ„Ī»ĆæĆėŗĶ![]() øöµ„Ī»ĆæĆėµÄĖŁ¶ČĻąĻņ¶ųŠŠ£¬Ōņ¼øĆėŗóA”¢CĮ½µćĻą¾ą
øöµ„Ī»ĆæĆėµÄĖŁ¶ČĻąĻņ¶ųŠŠ£¬Ōņ¼øĆėŗóA”¢CĮ½µćĻą¾ą![]() øöµ„Ī»³¤¶Č£æ
øöµ„Ī»³¤¶Č£æ
”¾“š°ø”æ(1)-7»ņ-1£»(2)-4-![]() t£¬4+t£»(3)²»±ä£¬¶ØÖµĪŖ4£»(4)t=2»ņt=
t£¬4+t£»(3)²»±ä£¬¶ØÖµĪŖ4£»(4)t=2»ņt=![]() .
.
”¾½āĪö”æ
£Ø1£©øł¾Ż·ĒøŗŹżµÄŠŌÖŹĒó³öa”¢bµÄÖµ£¬ŌŁÓɾąĄėµÄ¶ØŅåĒó½ā¼“æÉ£»
£Ø2£©øł¾ŻĢāŅā±ķŹ¾³öµć![]() ”¢
Ӣ![]() Ӣ
”¢![]() Ėł±ķŹ¾µÄŹż£¬¼“æÉµĆ³ö½įĀŪ£»
Ėł±ķŹ¾µÄŹż£¬¼“æÉµĆ³ö½įĀŪ£»
£Ø3£©ĻČĒó³ö![]() £¬Č»ŗó“śČė»Æ¼ņ¼“æÉµĆ³ö½įĀŪ£»
£¬Č»ŗó“śČė»Æ¼ņ¼“æÉµĆ³ö½įĀŪ£»
£Ø4£©Ēó³öµćAµÄĀ·³ĢĪŖ4t£¬µćCµÄĀ·³ĢĪŖ2t£¬Č»ŗó·ÖĪŖĻąÓöĒ°Ļą¾ą![]() øöµ„Ī»³¤¶ČŗĶĻąÓöŗóĻą¾ą
øöµ„Ī»³¤¶ČŗĶĻąÓöŗóĻą¾ą![]() øöµ„Ī»³¤¶ČĮŠ·½³Ģ£¬Ēó½ā¼“æÉ£®
øöµ„Ī»³¤¶ČĮŠ·½³Ģ£¬Ēó½ā¼“æÉ£®
£Ø1£©ÓÉ·ĒøŗŹżµÄŠŌÖŹæɵƵ½£ŗa+4=0£¬b£2=0£¬½āµĆ£ŗa=£4£¬b=2£®
ÉčD±ķŹ¾µÄŹżĪŖx£¬ŌņAD=x££Ø£4£©=3»ņ£4£x=3£¬½āµĆ£ŗx=£1»ņx=£7£®
¹Ź“š°øĪŖ£ŗ£7»ņ£1£®
£Ø2£©ÓÉĢāŅāæÉÖŖ£ŗµć![]() ±ķŹ¾µÄŹżŹĒ£ŗ
±ķŹ¾µÄŹżŹĒ£ŗ![]() £¬µć
£¬µć![]() ±ķŹ¾µÄŹżŹĒ£ŗ
±ķŹ¾µÄŹżŹĒ£ŗ![]() £¬µć
£¬µć![]() ±ķŹ¾µÄŹżŹĒ£ŗ
±ķŹ¾µÄŹżŹĒ£ŗ![]() £¬”ą
£¬”ą![]() =
=![]() ££Ø
££Ø![]() £©=
£©=![]() =
=![]() £®
£®
¹Ź“š°øĪŖ£ŗ![]() £¬
£¬![]() £®
£®
£Ø3£©ÓÉ£Ø2£©µĆ£ŗ![]() =
= ![]() ££Ø
££Ø![]() £©=
£©=![]() =
=![]() £¬”ą
£¬”ą![]() =
=![]() =
=![]() =4£®¹Ź
=4£®¹Ź![]() ĪŖ¶ØÖµ4£®
ĪŖ¶ØÖµ4£®
£Ø4£©ÓÉĢāŅāµĆ£ŗµćAµÄĀ·³ĢĪŖ4t£¬µćCµÄĀ·³ĢĪŖ2t£¬”ą4t+2t=10+2»ņ4t+2t=10£2£¬½āµĆ£ŗt=2»ņt=![]() £®
£®


 »ĘøŌŠ”דŌŖ½ā¾öĪŹĢāĢģĢģĮ·ĻµĮŠ“š°ø
»ĘøŌŠ”דŌŖ½ā¾öĪŹĢāĢģĢģĮ·ĻµĮŠ“š°ø ČżµćŅ»²āæģĄÖÖÜ¼Ę»®ĻµĮŠ“š°ø
ČżµćŅ»²āæģĄÖÖÜ¼Ę»®ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĪŖ½ØÉčĆĄĄöÅ©“壬“åĪÆ»į“ņĖćŌŚÕż·½ŠĪµŲæé¼×ŗĶ³¤·½ŠĪµŲæéŅŅÉĻ½ųŠŠĀĢ»Æ.ŌŚĮ½µŲæéÄŚ·Ö±š½ØŌģŅ»øö±ß³¤ĪŖaµÄ“óÕż·½ŠĪ»ØĢ³ŗĶĖÄøö±ß³¤ĪŖbµÄŠ”Õż·½ŠĪ»ØĢ³(ŅõÓ°²æ·Ö)£¬æÕ°×ĒųÓņĘĢÉč²ŻĘŗ£¬¼ĒS1±ķŹ¾µŲæé¼×ÖŠæհד¦ĘĢÉč²ŻĘŗµÄĆ껿£¬S2±ķŹ¾µŲæéŅŅÖŠæհד¦ĘĢÉč²ŻĘŗµÄĆ껿£®
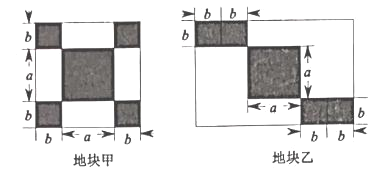
£Ø1£©S1=________£¬S2=________(ÓĆŗ¬a£¬bµÄ“śŹżŹ½±ķŹ¾²¢»Æ¼ņ) .
£Ø2£©Čōa=2b£¬ĒóµÄ![]() Öµ
Öµ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
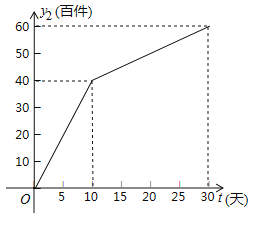
”¾ĢāÄæ”æ£Ø2017ŗž±±Ź”¾£ĆÅŹŠ£©ĪŅŹŠĄ×Ą×·žŹĪÓŠĻŽ¹«Ė¾Éś²śĮĖŅ»æīĻļ¾·ž×°£¬ĶعżŹµĢåÉĢµźŗĶĶųÉĻÉĢµźĮ½ÖÖĶ¾¾¶½ųŠŠĻśŹŪ£¬ĻśŹŪŅ»¶ĪŹ±¼äŗó£¬øĆ¹«Ė¾¶ŌÕāÖÖÉĢĘ·µÄĻśŹŪĒéæö£¬½ųŠŠĮĖĪŖĘŚ30ĢģµÄøś×Łµ÷²é£¬ĘäÖŠŹµĢåÉĢµźµÄČÕĻśŹŪĮæy1£Ø°Ł¼ž£©ÓėŹ±¼ät£ØtĪŖÕūŹż£¬µ„Ī»£ŗĢģ£©µÄ²æ·Ö¶ŌÓ¦ÖµČēĻĀ±ķĖłŹ¾£¬ĶųÉĻÉĢµźµÄČÕĻśŹŪĮæy2£Ø°Ł¼ž£©ÓėŹ±¼ät£ØtĪŖÕūŹż£¬µ„Ī»£ŗĢģ£©µÄ²æ·Ö¶ŌÓ¦ÖµČēĶ¼ĖłŹ¾£®
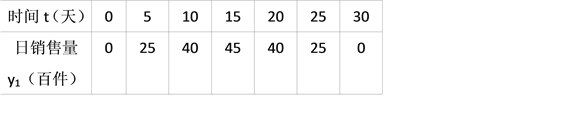
£Ø1£©ĒėÄćŌŚŅ»“ĪŗÆŹż”¢¶ž“ĪŗÆŹżŗĶ·“±ČĄżŗÆŹżÖŠ£¬Ń”ŌńŗĻŹŹµÄŗÆŹżÄÜ·“Ó³y1ÓėtµÄ±ä»Æ¹ęĀÉ£¬²¢Ēó³öy1ÓėtµÄŗÆŹż¹ŲĻµŹ½¼°×Ō±äĮætµÄȔֵ·¶Ī§£»
£Ø2£©Ēóy2ÓėtµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³ö×Ō±äĮætµÄȔֵ·¶Ī§£»
£Ø3£©ŌŚøś×Łµ÷²éµÄ30ĢģÖŠ£¬É菵ĢåÉĢµźŗĶĶųÉĻÉĢµźµÄČÕĻśŹŪ×ÜĮæĪŖy£Ø°Ł¼ž£©£¬ĒóyÓėtµÄŗÆŹż¹ŲĻµŹ½£»µ±tĪŖŗĪÖµŹ±£¬ČÕĻśŹŪ×ÜĮæy“ļµ½×ī“󣬲¢Ēó³ö“ĖŹ±µÄ×ī“óÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļßy=kx+6·Ö±šÓėxÖį”¢yÖį½»ÓŚµćE£¬F£¬ŅŃÖŖµćEµÄ×ų±źĪŖ£Ø©8£¬0£©£¬µćAµÄ×ų±źĪŖ£Ø©6£¬0£©£®
£Ø1£©ĒókµÄÖµ£»
£Ø2£©ČōµćP£Øx£¬y£©ŹĒøĆÖ±ĻßÉĻµÄŅ»øö¶Æµć£¬ĒŅŌŚµŚ¶žĻóĻŽÄŚŌĖ¶Æ£¬ŹŌŠ“³ö”÷OPAµÄĆ껿S¹ŲÓŚxµÄŗÆŹż½āĪöŹ½£¬²¢Š“³ö×Ō±äĮæxµÄȔֵ·¶Ī§£®
£Ø3£©Ģ½¾æ£ŗµ±µćPŌĖ¶Æµ½Ź²Ć“Ī»ÖĆŹ±£¬”÷OPAµÄĆ껿ĪŖ![]() £¬²¢ĖµĆ÷ĄķÓÉ£®
£¬²¢ĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼,ŹżÖįÉĻĻ߶Ī![]() (µ„Ī»³¤¶Č),Ļ߶Ī
(µ„Ī»³¤¶Č),Ļ߶Ī![]() (µ„Ī»³¤¶Č),µć
(µ„Ī»³¤¶Č),µć![]() ŌŚŹżÖįÉĻ±ķŹ¾µÄŹżŹĒ-10,µć
ŌŚŹżÖįÉĻ±ķŹ¾µÄŹżŹĒ-10,µć![]() ŌŚŹżÖįÉĻ±ķŹ¾µÄŹżŹĒ16,ČōĻ߶Ī
ŌŚŹżÖįÉĻ±ķŹ¾µÄŹżŹĒ16,ČōĻ߶Ī![]() ŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņÓŅŌČĖŁŌĖ¶Æ,Ķ¬Ź±Ļ߶Ī
ŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņÓŅŌČĖŁŌĖ¶Æ,Ķ¬Ź±Ļ߶Ī![]() ŅŌĆæĆė3øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņ×óŌČĖŁŌĖ¶Æ,ÉčŌĖ¶ÆŹ±¼äĪŖ
ŅŌĆæĆė3øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņ×óŌČĖŁŌĖ¶Æ,ÉčŌĖ¶ÆŹ±¼äĪŖ![]() Ćė
Ćė
(1)µ±µć![]() Óėµć
Óėµć![]() ĻąÓöŹ±,µć
ĻąÓöŹ±,µć![]() ”¢µć
”¢µć![]() ŌŚŹżÖįÉĻ±ķŹ¾µÄŹż·Ö±šĪŖ £»
ŌŚŹżÖįÉĻ±ķŹ¾µÄŹż·Ö±šĪŖ £»
(2)µ±![]() ĪŖŗĪÖµŹ±,µć
ĪŖŗĪÖµŹ±,µć![]() øÕŗĆŹĒ
øÕŗĆŹĒ![]() µÄÖŠµć
µÄÖŠµć

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖĻĀĮŠ·½³Ģ£ŗ¢Ł![]() £»¢Ś0.3x£½1£»¢Ū
£»¢Ś0.3x£½1£»¢Ū![]() £»¢Üx2©4x£½3£»¢Żx£½6£»¢Žx+2y£½0£®ĘäÖŠŅ»ŌŖŅ»“Ī·½³ĢµÄøöŹżŹĒ£Ø””””£©
£»¢Üx2©4x£½3£»¢Żx£½6£»¢Žx+2y£½0£®ĘäÖŠŅ»ŌŖŅ»“Ī·½³ĢµÄøöŹżŹĒ£Ø””””£©
A. 2B. 3C. 4D. 5
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
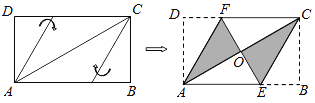
”¾ĢāÄæ”潫¾ŲŠĪ![]() °“ČēĶ¼ĖłŹ¾µÄ·½Ź½ÕŪµž£¬µĆµ½ĮāŠĪ
°“ČēĶ¼ĖłŹ¾µÄ·½Ź½ÕŪµž£¬µĆµ½ĮāŠĪ![]() £¬Čō
£¬Čō![]() £¬ŌņĮāŠĪ
£¬ŌņĮāŠĪ![]() µÄÖܳ¤ĪŖ______.
µÄÖܳ¤ĪŖ______.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬½«Ņ»æéŗ¬ÓŠ45”ć½ĒµÄÖ±½ĒČż½Ē°åČēĶ¼·ÅÖĆ£¬Ö±½Ē¶„µćCµÄ×ų±źĪŖ£Ø1£¬0£©£¬¶„µćAµÄ×ų±źĪŖ£Ø0£¬2£©£¬¶„µćBĒ”ŗĆĀäŌŚµŚŅ»ĻóĻŽµÄĖ«ĒśĻßÉĻ£¬ĻÖ½«Ö±½ĒČż½Ē°åŃŲxÖįÕż·½ĻņĘ½ŅĘ£¬µ±¶„µćAĒ”ŗĆĀäŌŚøĆĖ«ĒśĻßÉĻŹ±Ķ£Ö¹ŌĖ¶Æ£¬Ōņ“ĖŹ±µćCµÄ¶ŌÓ¦µćC”äµÄ×ų±źĪŖ ______________.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/4/1916730188324864/1920418179735552/STEM/955c40623e644964ae11bcb49c75f843.png]
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĄūĆńÉĢ³”¾ÓŖijÖÖĘ·ÅʵÄTŠō£¬¹ŗ½ųŹ±µÄµ„¼ŪŹĒ300ŌŖ£¬øł¾ŻŹŠ³”µ÷²é£ŗŌŚŅ»¶ĪŹ±¼äÄŚ£¬ĻśŹŪµ„¼ŪŹĒ400ŌŖŹ±£¬ĻśŹŪĮæŹĒ60¼ž£¬ĻśŹŪµ„¼ŪĆæÕĒ10ŌŖ£¬ĻśŹŪĮæ¾Ķ¼õÉŁ1¼ž£®ÉčÕāÖÖTŠōµÄĻśŹŪµ„¼ŪĪŖxŌŖ£Øx£¾400£©Ź±£¬ĻśŹŪĮæĪŖy¼ž”¢ĻśŹŪĄūČóĪŖWŌŖ£®
£Ø1£©Ēė·Ö±šÓĆŗ¬xµÄ“śŹżŹ½±ķŹ¾yŗĶW£Ø°Ń½į¹ūĢīČėĻĀ±ķ£©£ŗ
ĻśŹŪµ„¼Ū£ØŌŖ£© | x |
ĻśŹŪĮæy£Ø¼ž£© | |
ĻśŹŪĄūČóW£ØŌŖ£© |
£Ø2£©øĆÉĢ³”¼Ę»®ŹµĻÖĻśŹŪĄūČó10000ŌŖ£¬²¢¾”æÉÄÜŌö¼ÓĻśŹŪĮ棬ÄĒĆ“xµÄÖµÓ¦µ±ŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com