
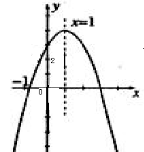
 的图象如图所示,则下列式子中①
的图象如图所示,则下列式子中① ;②
;② ;③
;③ ; ④
; ④ 成立的个数有( )
成立的个数有( ) 
| A.1个 | B.2个 | C.3个 | D.4个 |
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
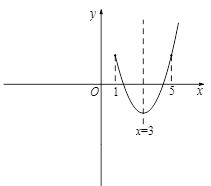
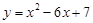 的最大值.他画图研究后发现,
的最大值.他画图研究后发现,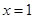 和
和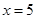 时的函数值相等,于是他认为需要对
时的函数值相等,于是他认为需要对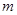 进行分类讨论.
进行分类讨论.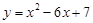 的对称轴为直线
的对称轴为直线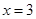 ,
,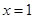 和
和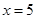 时的函数值相等.
时的函数值相等.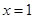 时,
时,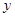 的最大值为2;
的最大值为2;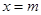 时,
时,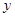 的最大值为
的最大值为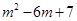 .
.
 ≤x≤4时,二次函数
≤x≤4时,二次函数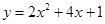 的最大值为_______;
的最大值为_______;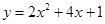 的最大值;
的最大值;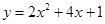 的最大值为31,则
的最大值为31,则 的值为_______.
的值为_______.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
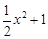 、y=
、y=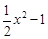 所截.当直线L向右平移2个单位时,直线L被两条抛物线所截得的线段扫过的图形面积为 __ 平方单位。
所截.当直线L向右平移2个单位时,直线L被两条抛物线所截得的线段扫过的图形面积为 __ 平方单位。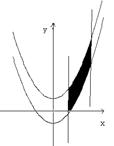
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com