
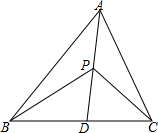
 如图,△ABC中,AB>AC,AD是∠A的平分线,点P是线段AD上的任意一点,则AB+PC与AC+PB的大小关系是( )
如图,△ABC中,AB>AC,AD是∠A的平分线,点P是线段AD上的任意一点,则AB+PC与AC+PB的大小关系是( )| A、AB+PC>AC+PB |
| B、AB+PC<AC+PB |
| C、AB+PC=AC+PB |
| D、不确定 |
|


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 (1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O上一动点,求PA的最大值和最小值.
(1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O上一动点,求PA的最大值和最小值. |
| AC |
 |
| CB |
查看答案和解析>>
科目:初中数学 来源: 题型:
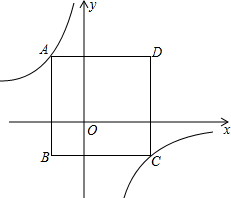 如图,边长为6的正方形ABCD置于平面直角坐标系xOy中,且AB平行于y轴,已知点A的横坐标为-2,反比例函数y=
如图,边长为6的正方形ABCD置于平面直角坐标系xOy中,且AB平行于y轴,已知点A的横坐标为-2,反比例函数y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
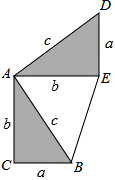 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中常见的是“面积法”,当两个全等的直角三角形如图摆放时(其中∠DAB=90°),就可以用“面积法”来证明勾股定理,即证明a2+b2=c2,请你写出勾股定理的证明过程.
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中常见的是“面积法”,当两个全等的直角三角形如图摆放时(其中∠DAB=90°),就可以用“面积法”来证明勾股定理,即证明a2+b2=c2,请你写出勾股定理的证明过程.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点D是△ABC的两外角平分线的交点,下列说法:
如图,点D是△ABC的两外角平分线的交点,下列说法:| A、②④④ | B、①②④ |
| C、②③④ | D、①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com