
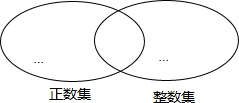
 如图两个圈分别表示正数集和整数集,请找出9个数填入这两个圈中,使其中每个圈正好6个数,你能说出这两个圈的重叠部分表示什么数的集合吗?
如图两个圈分别表示正数集和整数集,请找出9个数填入这两个圈中,使其中每个圈正好6个数,你能说出这两个圈的重叠部分表示什么数的集合吗? 科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,CO⊥AB于点O,D在⊙O上,连接BD、CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.
如图,AB为⊙O的直径,CO⊥AB于点O,D在⊙O上,连接BD、CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
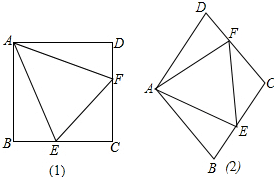 (1)如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.
(1)如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
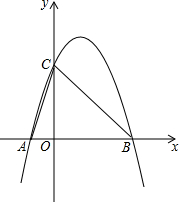 如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2-2ax-3a的图象与x轴交于A、B两点(点B在点A的右侧),交y轴于点C,且S△ABC=6
如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2-2ax-3a的图象与x轴交于A、B两点(点B在点A的右侧),交y轴于点C,且S△ABC=6查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (p5q4)÷(2p3q)=2p2q3 | B. | (-a+5)(-a-5)=-a2-25 | ||
| C. | $\frac{1}{a}+\frac{2}{a}=\frac{3}{2a}$ | D. | $\frac{2a}{{{a^2}-4}}-\frac{1}{a-2}=\frac{1}{a+2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com