
【题目】在平面直角坐标系中,点A(a ,2![]() )是直线y=
)是直线y=![]() x上一点,以A为圆心,2为半径作⊙A,若P(x,y)是第一象限内⊙A上任意一点,则
x上一点,以A为圆心,2为半径作⊙A,若P(x,y)是第一象限内⊙A上任意一点,则![]() 的最小值为( )
的最小值为( )
A. 1 B. ![]() C.
C. ![]() —1 D.
—1 D. ![]()
【答案】D
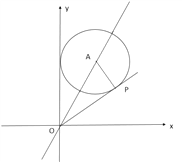
【解析】分析: 如图所示,当直线OP与圆A相切时,连接AP,过P作PH⊥x轴,此时![]() 取得最小值,利用切线的性质得到AP垂直于OP,在直角三角形AOP中,根据到角两边距离相等的点在角的平分线上确定出∠AOP=30°,
取得最小值,利用切线的性质得到AP垂直于OP,在直角三角形AOP中,根据到角两边距离相等的点在角的平分线上确定出∠AOP=30°,![]() 为tan∠30°的值,求出即可.
为tan∠30°的值,求出即可.
详解: 如图所示,当直线OP与圆A相切时,连接AP,过P作PH⊥x轴,此时![]() 取得最大值,
取得最大值,
∵点A(a ,2![]() )是直线y=
)是直线y=![]() x上一点,
x上一点,
∴a=2,
∴A(2 ,2![]() ).
).
∵以A为圆心,2为半径作⊙A,
∴⊙A与y轴相切.
则当直线OP与圆A相切时, ![]() 取得最小值,
取得最小值,
∵∠AOy=∠AOP=30°,
∴∠AOx=30°,
∴此时![]() =tan30°=
=tan30°=![]() ,
,
则![]() 的最小值为
的最小值为![]() .
.
故选:D.
点睛:
此题考查了切线的性质,坐标与图形性质,以及锐角三角函数定义,熟练掌握切线的性质是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,射线OM上有三点A,B,C,满足OA=20cm,AB=60cm,BC=10cm,动点P从O点出发沿OM方向以每秒1cm的速度匀速运动;动点Q从点C出发,在线段CO上向点O匀速运动(点Q运动到点O时,立即停止运动),点P,Q同时出发.
(1)当点P与点Q都同时运动到线段AB的中点时,求点Q的运动速度;
(2)若点Q运动速度为每秒3cm时,经过多少时间P,Q两点相距70cm;
(3)当PA=2PB时,点Q运动的位置恰好是线段AB的三等分,求点Q的速度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方法感悟:
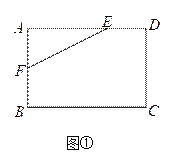
(1)如图①,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,是否在边BC、CD上分别存在点G、H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.
问题解决:
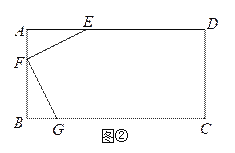
(2)如图②,有一矩形板材ABCD,AB=3米,AD=6米,现想从此板材中裁出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,EF=FG=![]() 米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积,并写出在以B为坐标原点,直线BC为x轴,直线BA为y轴的坐标系中,点H的坐标;若不能,请说明理由.
米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积,并写出在以B为坐标原点,直线BC为x轴,直线BA为y轴的坐标系中,点H的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点A对应的数是﹣1,B点对应的数是1,一只小虫甲从点B出发沿着数轴的正方向以每秒4个单位的速度爬行至C点,再立即返回到A点,共用了4秒钟.
(1)求点C对应的数;
(2)若小虫甲返回到A点后再作如下运动:第1次向右爬行2个单位,第2次向左爬行4个单位,第3次向右爬行6个单位,第4次向左爬行8个单位,…依次规律爬下去,求它第10次爬行所停在点所对应的数;
(3)若小虫甲返回到A后继续沿着数轴的负方向以每秒4个单位的速度爬行,这时另一小虫乙从点C出发沿着数轴的负方向以每秒7个单位的速度爬行,设甲小虫对应的点为E点,乙小虫对应的点为F点,设点A、E、F、B所对应的数分别是xA、xE、xF、xB,当运动时间t不超过1秒时,请你结合数轴求出 |xA﹣xE |﹣|xE﹣xF |+ |xF﹣xB |= .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们的平均亩产量分别是![]() =610千克,
=610千克, ![]() =609千克,亩产量的方差分别是
=609千克,亩产量的方差分别是![]() =29.6,
=29.6, ![]() =2.则关于两种小麦推广种植的合理决策是( )
=2.则关于两种小麦推广种植的合理决策是( )
A. 甲的平均亩产量较高,应推广甲
B. 甲、乙的平均亩产量相差不多,均可推广
C. 甲的平均亩产量较高,且亩产量比较稳定,应推广甲
D. 甲、乙的平均亩产量相差不多,但乙的亩产量比较稳定,应推广乙
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AE、CF分别被直线EF、AC所截,已知,∠1=∠2,AB平分∠EAC,CD平分∠ACG.将下列证明AB∥CD的过程及理由填写完整.
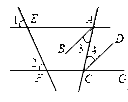
证明:∵ ∠1="∠2" ( 已知 )
∴ AE∥ ( )
∴ ∠EAC =∠ ,( )
而AB平分∠EAC,CD平分∠ACG( 已知 )
∴∠ =![]() ∠EAC,∠4=
∠EAC,∠4=![]() ∠ ( 角平分线的定义 )
∠ ( 角平分线的定义 )
∴∠ =∠4(等量代换)
∴AB∥CD( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A,B两点对应的数分别-4,8.有一动点P从点A出发第一次向左运动1个单位长度;然后在新的位置第二次运动,向右运动2个单位长度;在此位置第三次运动,向左运动3个单位长度,…按照如此规律不断地左右运动
![]()
(1)当运动到第2018次时,求点P所对应的有理数.
(2)点P会不会在某次运动时恰好到达某一个位置,使点P到点B的距离是点P到点A的距离的3倍?若可能请求出此时点P的位置,若不可能请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,垂足为点E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.

(1)若CF=2,AE=3,求BE的长;
(2)求证:∠CEG=![]() ∠AGE.
∠AGE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市绿化部门决定利用现有的不同种类花卉搭配园艺造型,摆放于城区主要大道的两侧.A、B两种园艺造型均需用到杜鹃花,A种造型每个需用杜鹃花25盆,B种造型每个需用杜鹃花35盆,解答下列问题:
(1)已知人民大道两侧搭配的A、B两种园艺造型共60个,恰好用了1700盆杜鹃花,A、B两种园艺造型各搭配了多少个?
(2)如果搭配一个A种造型的成本W与造型个数![]() 的关系式为:W=100―
的关系式为:W=100―![]() x (0<x<50),搭配一个B种造型的成本为80元.现在观海大道两侧也需搭配A、B两种园艺造型共50个,要求每种园艺造型不得少于20个,并且成本总额y(元)控制在4500元以内. 以上要求能否同时满足?请你通过计算说明理由.
x (0<x<50),搭配一个B种造型的成本为80元.现在观海大道两侧也需搭配A、B两种园艺造型共50个,要求每种园艺造型不得少于20个,并且成本总额y(元)控制在4500元以内. 以上要求能否同时满足?请你通过计算说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com