
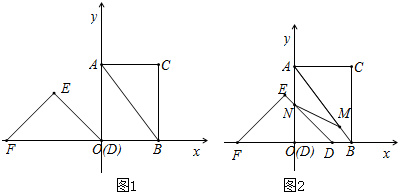
分析 (1)首先求出A、B两点的坐标是多少;然后应用待定系数法,求出AB的解析式即可.
(2)首先作EG⊥x轴于点G,求出GO的长度是多少;再根据时间=路程÷速度,用GO的长度除以△EFD的运动速度,求出当点E在AD上时,t的值是多少;然后作EH⊥y轴于点H,求出EH的长度是多少;再根据时间=路程÷速度,用GO的长度与EH的长度和除以△EFD的运动速度,求出当点E在AB上时,t的值是多少即可.
(3)根据题意,分4种情况:①当0<t≤5时;②当5<t≤6时;③当6<t≤$\frac{29}{4}$时;④当$\frac{29}{4}$<t≤9时;分类讨论,求出△EFD与△AOB重叠部分面积S与t的函数关系式及相应自变量t的取值范围即可.
(4)根据题意,分两种情况:Ⅰ、当0<t≤5时;Ⅱ、当5<t≤9时;分类讨论,根据△AMN为直角三角形,求出t的值是多少即可.
解答 解:(1)∵OA=8,OB=6,
∴A点的坐标是(0,8),B两点的坐标是(6,0),
设AB的解析式为:y=kx+b
则$\left\{\begin{array}{l}8=b\\ 0=6k+b\end{array}\right.$
解得:$\left\{\begin{array}{l}k=-\frac{4}{3}\\ b=8\end{array}\right.$
∴AB的解析式为:$y=-\frac{4}{3}x+8$.
(2)①如图1,作EG⊥x轴于点G,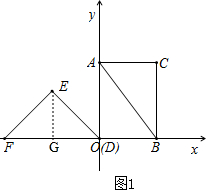 ,
,
∵△EFD是等腰直角三角形,
∴点G是FD的中点,
∴GO=10÷2=5,
∴当点E在AD上时,
t=5÷1=5(s);
②如图2,作EH⊥y轴于点H, ,
,
∵EH∥FD,
∴$\frac{EH}{OB}=\frac{AH}{AO}=\frac{8-5}{8}=\frac{3}{8}$,
∴EH=OB×$\frac{3}{8}$=6×$\frac{3}{8}=\frac{9}{4}$,
∴当E在AC上时,
t=(5$+\frac{9}{4}$)÷1=$\frac{29}{4}$(s).
(3)①如图3, ,
,
当0<t≤5时,
OD=t,
∵∠PDO=45°,
∴OP=OD=t,
∴S=$\frac{1}{2}$t2
②如图4,作EM⊥x轴于点M,EF与y轴交与点N, ,
,
当5<t≤6时,
FO=FD-OD=10-t,
∵∠NFO=45°,
∴NO=FO=10-t,
∴S=S△EFD-S△NOF
=10×$5÷2-\frac{1}{2}(10-t)(10-t)$
=25-$\frac{1}{2}$t2+10t-50
=-$\frac{1}{2}$t2+10t-25
③如图5,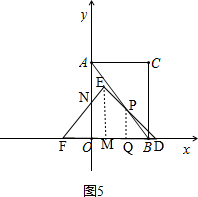 ,
,
FO=FD-OD=10-t,
∵∠NFO=45°,
∴NO=FO=10-t,
设PQ=x,
则QD=x,
∵$\frac{x}{QB}=\frac{8}{6}$,
∴QB=$\frac{3}{4}x$,
∴BD=QD-QB=x-$\frac{3}{4}x=\frac{1}{4}x=t-6$,
∴x=4t-24,
∴S=S△EFD-S△FNO-S△PBD
=10×5÷2$-\frac{1}{2}$(10-t)2$-\frac{1}{2}$×$\frac{1}{4}x•x$
=25-$\frac{1}{2}$t2+10t-50$-\frac{1}{8}$×(4t-24)2
=-$\frac{1}{2}$t2+10t-25-2t2+24t-72
=-$\frac{5}{2}$t2+34t-97
④如图6,作HI⊥x轴于点I,EF与y轴交与点N, ,
,
∵OA=8,OB=6,
∴AB=$\sqrt{{8}^{2}{+6}^{2}}=10$,
∴当M到达点C时,需要的时间是:
(10+8)÷2=18÷2=9(s),
当$\frac{29}{4}$<t≤9时,
FO=FD-OD=10-t,
∵∠NFO=45°,
∴NO=FO=10-t,
设HI=x,
则FI=x,BI=$\frac{3}{4}x$,
∴x$+\frac{3}{4}x=10-t+6=16-t$,
解得x=$\frac{4}{7}(16-t)$,
∴S=$\frac{4}{7}(16-t)×(16-t)×\frac{1}{2}$$-\frac{1}{2}$(10-t)2
=$\frac{2}{7}×$(t2-32t+256)$-\frac{1}{2}$t2+10t-50
=-$\frac{3}{14}$t2+$\frac{6}{7}t$+$\frac{162}{7}$
综上,可得
S=$\left\{\begin{array}{l}\frac{1}{2}{t^2}(0<t≤5)\\-\frac{1}{2}{t^2}+10t-25(5<t≤6)\\-\frac{5}{2}{t^2}+34t-97(6<t≤\frac{29}{4})\\-\frac{3}{14}{t^2}+\frac{6}{7}t+\frac{162}{7}(\frac{29}{4}<t≤9)\end{array}\right.$
(4)Ⅰ、当0<t≤5时,可得∠MAN≠90,AM=2t,AN=8-t,
①若∠AMN=90°,
则$\frac{4}{5}(8-t)=2t$,
∴$t=\frac{16}{7}$;
②若∠ANM=90°,
则$\frac{4}{5}•2t=8-t$,
∴$t=\frac{40}{13}$.
Ⅱ、当5<t≤9时,可得∠MAN≠90°,MH=3t-20,BM=18-2t,
①若∠AMN=90°,t不存在;
②若∠ANM=90°,
则此时M,H重合,
∴3t-20=0,
∴t=$\frac{20}{3}$.
综上,可得当t的值为$\frac{16}{7},\frac{40}{13},\frac{20}{3}$时,△AMN为直角三角形.
故答案为:5、$\frac{29}{4}$.
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握.
(3)此题还考查了三角形的面积的求法,以及勾股定理的应用,要熟练掌握.


 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 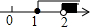 | B. | 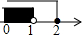 | C. | 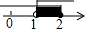 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
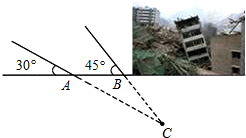 2015年4月25日14时11分,尼泊尔发生8.1级地震,震源深度20千米.中国救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧某面上选两探测点A、B,AB相距2米,探测线与该面的夹角分别是30°和45°(如图).试确定生命所在点C与探测面的距离.(参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
2015年4月25日14时11分,尼泊尔发生8.1级地震,震源深度20千米.中国救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧某面上选两探测点A、B,AB相距2米,探测线与该面的夹角分别是30°和45°(如图).试确定生命所在点C与探测面的距离.(参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥$\frac{1}{2}$ | B. | x≤1 | C. | $\frac{1}{2}$≤x≤1 | D. | 以上答案都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这组数据的平均数是75 | B. | 这组数据的中位数是74 | ||
| C. | 这组数据的方差是3.2 | D. | 这组数据的众数是76 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com