
【题目】如图,CE是平行四边形ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E,连接AC,BE,则下列结论:①AC=AD;②AO=![]() ;③四边形ACBE是菱形;④
;③四边形ACBE是菱形;④![]() .其中正确的结论有____.(填写所有正确结论的序号)
.其中正确的结论有____.(填写所有正确结论的序号)

【答案】①②③④;
【解析】
根据平行四边形的性质以及判定定理、菱形的判定方法、平行线分线段成比例定理一一判断即可;
解:解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD(平行四边形对边相等且平行),
∵EC垂直平分AB,
∴![]() ,故②正确,
,故②正确,
∴![]() ,
,
∵OA∥DC,
![]() ,
,
∴AE=AD,OE=OC,
∵OA=OB,OE=OC,
∴四边形ACBE是平行四边形(对角线相互平分的四边形是平行四边形),
∵AB⊥EC,
∴四边形ACBE是菱形(对角线相互垂直的四边形是菱形),故③正确,
∵∠DCE=90°,DA=AE,
∴AC=AD=AE,故①正确;
∵![]() ,
,
![]() ,
,
∴![]() ,故④正确;
,故④正确;
综上①②③④均正确,
故答案为:①②③④;


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm.点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动,设运动时间为x秒,△PBQ的面积为y(cm2).

(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N.连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】补全解答过程:
已知:如图,直线AB∥CD,直线EF与直线AB,CD分别交于点G,H;GM平分∠FGB,∠3=60°.求∠1的度数.
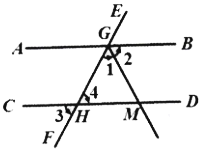
解:∵EF与CD交于点H,(已知)
∴∠3=∠4.( )
∵∠3=60°,(已知)
∴∠4=60°.( )
∵AB∥CD,EF与AB,CD交于点G,H,(已知)
∴∠4+∠FGB=180°.( )
∴∠FGB= .
∵GM平分∠FGB,(已知)
∴∠1= °.(角平分线的定义)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在![]() 中,已知AB=AC,垂足为点D,点F在AD的延长线上,且CE∥BF,试说明DE=DF的理由.
中,已知AB=AC,垂足为点D,点F在AD的延长线上,且CE∥BF,试说明DE=DF的理由.

解:因为AB=AC,AD⊥BC(已知)
所以BD=
因为CE∥BF(已知)
所以![]() =
=
在![]() 中,
中,
![]() 中
中
=
=
所以![]() ( )
( )
所以DE=DF( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型企业为了保护环境,准备购买A、B两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购买A型2台、B型3台需54万,购买A型4台、B型2台需68万元.
(1)求出A型、B型污水处理设备的单价;
(2)经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1565吨,请你为该企业设计一种最省钱的购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com